U-tiling: UQC408

h-net
1 record listed.
| Image |
h-net name |
Orbifold symbol |
Transitivity (Vert,Edge,Face) |
Vertex Degree |
2D Vertex Symbol |
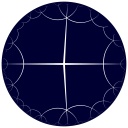 |
hqc481 |
*222222 |
(2,4,2) |
{4,6} |
{6.8.8.6}{6.8.8.6.8.8} |
s-nets
3 records listed.
| Surface |
Edge collapse |
Image |
s-net name |
Other names |
Space group |
Space group number |
Symmetry class |
Vertex degree(s) |
Vertices per primitive unit cell |
Transitivity (Vertex, Edge) |
|
P
|
False
|

|
sqc1413
|
|
Cmma |
67 |
orthorhombic |
{6,4} |
6 |
(2,4) |
|
G
|
False
|
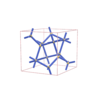
|
sqc1410
|
|
C2/c |
15 |
monoclinic |
{6,4} |
6 |
(2,5) |
|
D
|
False
|
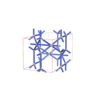
|
sqc1411
|
|
Imma |
74 |
orthorhombic |
{6,4} |
6 |
(2,4) |
Topological data
| Vertex degrees | {4,6} |
| 2D vertex symbol | {6.8.8.6}{6.8.8.6.8.8} |
| Dual tiling |  |
D-symbol
Genus-3 version with t-tau cuts labelled
<6.2:56:29 4 5 41 21 43 11 12 55 28 50 18 19 48 36 25 26 34 32 33 56 39 40 49 46 47 53 54,2 10 6 7 9 13 14 16 24 20 21 23 27 28 30 45 34 35 37 52 41 42 44 48 49 51 55 56,15 3 5 34 35 22 10 12 48 49 17 19 55 56 24 26 41 42 50 31 33 43 38 40 45 47 52 54:8 6 8 6,6 4 4 4 4 6> {(1, 44): 'tau1^-1', (1, 51): 'tau1', (2, 49): 't2^-1*tau3*t1*tau2^-1*t3^-1', (0, 47): 't2', (2, 21): 't1', (0, 28): 't3*tau2', (0, 40): 't3^-1', (0, 33): 't3', (0, 42): 't2*tau3^-1', (0, 54): 't2^-1', (0, 35): 't3^-1*tau2^-1', (2, 42): 't2*tau3^-1*t1^-1*tau2*t3', (2, 14): 't1', (0, 49): 't2^-1*tau3', }





