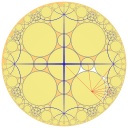
h-net: hqc2365
Topological data
| Orbifold symbol | *4444 |
| Transitivity (vertex, edge, ring) | (6,6,2) |
| Vertex degrees | {4,8,4,4,8,4} |
| 2D vertex symbol | {8.8.8.8}{8.8.8.8.8.8.8.8}{8.3.3.8}{8.8.3.3}{3.3.3.3.3.3.3.3}{8.8.8.8} |
| Vertex coordination sequence | [(4, 28, 84, 360, 892, 3828, 9660, 40720, 103972), (8, 24, 112, 288, 1232, 3096, 13080, 33344, 140552), (4, 14, 32, 148, 392, 1610, 4164, 17568, 45532), (4, 10, 28, 84, 316, 954, 3596, 10464, 38876, 112982), (8, 8, 40, 120, 488, 1256, 5304, 14144, 57288), (4, 12, 28, 72, 244, 996, 2924, 10736, 31476, 116380)] |
| Delaney-Dress Symbol | <2365.2:14:2 4 6 8 10 12 14,1 3 5 13 9 12 11 14,1 2 3 4 7 8 9 10 11 12 13 14:8 3,4 8 4 4 8 4> |
| Dual net | hqc2328 |
Derived s-nets
s-nets with faithful topology
4 records listed.| Image | s-net name | Other names | Space group | Space group number | Symmetry class | Vertex degree(s) | Vertices per primitive unit cell | Transitivity (Vertex, Edge) |
|---|---|---|---|---|---|---|---|---|
|
sqc6432 | P-4m2 | 115 | tetragonal | {4,8,4,4,8,4} | 12 | (6,6) | |
|
sqc6380 | I-4 | 82 | tetragonal | {4,8,4,4,8,4} | 12 | (6,7) | |
|
sqc6377 | I-4m2 | 119 | tetragonal | {4,8,4,4,8,4} | 12 | (6,6) | |
|
sqc6431 | I-4m2 | 119 | tetragonal | {4,8,4,4,8,4} | 12 | (6,6) |
s-nets with edge collapse
Derived U-tilings
2 records listed.| Image | U-tiling name | PGD Subgroup | Transitivity (Vert,Edge,Face) | Vertex Degree | Vertex Symbol | P net | G net | D net |
|---|---|---|---|---|---|---|---|---|
 |
UQC5915 | *4444 | (6,6,2) | {4,8,4,4,8,4} | {8.8.8.8}{8.8.8.8.8.8.8.8}{8.3.3... |
sqc5611
|
sqc6380
|
sqc6431
|
 |
UQC5916 | *4444 | (6,6,2) | {4,8,4,4,8,4} | {8.8.8.8}{8.8.8.8.8.8.8.8}{8.3.3... |
sqc6432
|
sqc6380
|
sqc6377
|
