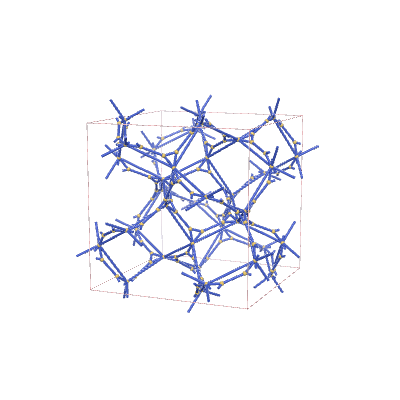
s-net: sqc13878

Barycentric geometry maximising unit cell volume Geometry favouring equal edge lengths (relaxed) Toggle geometry	Customizable net view on webGavrog Systre crystallographic geometry file (.cgd)

Links to this net in other databases

topcryst

Topological data

Vertices per primitive translational unit	60
Edges per primitive translational unit	120
Transitivity (vertex,edge)	(3,5)
Vertex degrees	{8,3,3}
Vertex coordination sequence	[(8, 28, 74, 152, 268, 414, 586, 776, 1012, 1278), (3, 8, 26, 73, 152, 268, 414, 586, 776, 1012), (3, 8, 26, 73, 152, 268, 414, 586, 776, 1012)]
Wells’ vertex symbol	[3^2.4^4.5^4.6^6.8^8.10^4, 3.4.5, 3.4.5]
Systre key	(3, 1, 2, 0, 0, 0, 1, 3, 0, 0, 0, 1, 4, 0, 0, 0, 1, 5, 0, 0, 0, 1, 6, 0, 0, 0, 1, 7, 0, 0, 0, 1, 8, 0, 0, 0, 1, 9, 0, 0, 0, 2, 10, 0, 0, 0, 2, 11, 0, 0, 0, 2, 12, 0, 0, 0, 2, 13, 0, 0, 0, 2, 14, 0, 0, 0, 2, 15, 0, 0, 0, 2, 16, 0, 0, 0, 3, 11, 1, 0, 0, 3, 17, 0, 0, 0, 3, 18, 0, 0, 0, 3, 19, 0, 0, 0, 3, 20, 0, 0, 0, 3, 21, 0, 0, 0, 3, 22, 0, 0, 0, 4, 5, 0, 0, 0, 4, 16, 0, 0, 0, 5, 23, 0, 0, 0, 6, 7, 0, 0, 0, 6, 20, 0, 0, 0, 7, 24, 0, 0, 0, 8, 11, 0, 0, 1, 8, 18, 0, 1, 0, 8, 22, -1, 0, 0, 8, 23, 0, 0, 0, 8, 25, 0, 0, 0, 8, 26, 0, 0, 0, 8, 27, 0, 0, 0, 9, 10, -1, -1, 1, 9, 11, 0, -1, 1, 9, 12, 0, 0, 1, 9, 24, 0, 0, 0, 9, 28, 0, 0, 0, 9, 29, 0, 0, 0, 9, 30, 0, 0, 0, 10, 31, 0, 0, 0, 10, 32, 0, 0, 0, 10, 33, 0, 0, 0, 10, 34, 0, 0, 0, 10, 35, 0, 0, 0, 10, 36, 0, 0, 0, 11, 37, 0, 0, 0, 11, 38, 0, 0, 0, 11, 39, 0, 0, 0, 11, 40, 0, 0, 0, 12, 31, -1, -1, 1, 12, 36, 0, -1, 0, 12, 41, 0, 0, 0, 12, 42, 0, 0, 0, 12, 43, 0, 0, 0, 12, 44, 0, 0, 0, 13, 16, 0, 0, 0, 13, 35, 0, 0, 0, 14, 15, 0, 0, 0, 14, 39, 0, 0, 0, 15, 43, 0, 0, 0, 17, 19, 0, 0, 0, 17, 40, 1, 0, 0, 18, 31, 0, -1, 1, 18, 36, 0, -1, 0, 18, 45, 0, 0, 0, 18, 46, 0, 0, 0, 18, 47, 0, 0, 0, 18, 48, 0, 0, 0, 19, 46, 0, 0, 0, 20, 21, 0, 0, 0, 21, 49, 0, 0, 0, 22, 31, 0, 0, 1, 22, 36, 0, -1, 1, 22, 49, 0, 0, 0, 22, 50, 0, 0, 0, 22, 51, 0, 0, 0, 22, 52, 0, 0, 0, 23, 25, 0, 0, 0, 24, 30, 0, 0, 0, 25, 48, 0, 1, 0, 26, 27, 0, 0, 0, 26, 51, -1, 0, 0, 27, 37, 0, 0, 1, 28, 29, 0, 0, 0, 28, 33, -1, -1, 1, 29, 38, 0, -1, 1, 30, 41, 0, 0, 1, 31, 53, 0, 0, 0, 31, 54, 0, 0, 0, 31, 55, 0, 0, 0, 31, 56, 0, 0, 0, 32, 33, 0, 0, 0, 32, 56, 0, 0, 0, 34, 35, 0, 0, 0, 34, 57, 0, 0, 0, 36, 57, 0, 0, 0, 36, 58, 0, 0, 0, 36, 59, 0, 0, 0, 36, 60, 0, 0, 0, 37, 38, 0, 0, 0, 39, 40, 0, 0, 0, 41, 42, 0, 0, 0, 42, 59, 0, -1, 0, 43, 44, 0, 0, 0, 44, 53, -1, -1, 1, 45, 48, 0, 0, 0, 45, 60, 0, -1, 0, 46, 47, 0, 0, 0, 47, 54, 0, -1, 1, 49, 52, 0, 0, 0, 50, 51, 0, 0, 0, 50, 55, 0, 0, 1, 52, 58, 0, -1, 1, 53, 54, 0, 0, 0, 55, 56, 0, 0, 0, 57, 60, 0, 0, 0, 58, 59, 0, 0, 0)

Geometric data

Systre equilibrium placement (barycentric embedding) maximising unit cell volume

Systre coordinates favouring equal edge-lengths

Hyperbolic sources

h-nets with faithful topology

1 record listed.

Image	h-net name	Orbifold symbol	Transitivity (Vert,Edge,Face)	Vertex Degree	2D Vertex Symbol
	hqc1393	*266	(2,4,4)	{3,8}	{12.4.3}{3.4.6.4.3.4.6.4}

h-nets with edge collapse

No items to display.