P222

Number	16
Symmetry Class	orthorhombic
Chiral	Y

s-nets

180 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
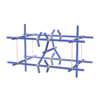
	sqc786		P222	16	orthorhombic	{4,4,8,4}	5	(4,6)
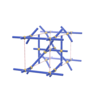
	sqc825		P222	16	orthorhombic	{4,4,4,4}	6	(4,7)
	sqc826		P222	16	orthorhombic	{3,3,4,4,4}	7	(5,6)
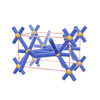
	sqc859		P222	16	orthorhombic	{10,4}	3	(2,6)
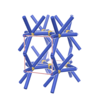
	sqc862		P222	16	orthorhombic	{4,10}	3	(2,6)
	sqc863		P222	16	orthorhombic	{9,6}	3	(2,6)
	sqc902		P222	16	orthorhombic	{6,3}	6	(2,6)
	sqc913		P222	16	orthorhombic	{4,4,4,3,6}	6	(5,6)
	sqc953		P222	16	orthorhombic	{4,4,4,4,4}	6	(5,6)
	sqc984		P222	16	orthorhombic	{4,10}	5	(2,6)
	sqc1001		P222	16	orthorhombic	{4,9}	4	(2,7)
	sqc1009		P222	16	orthorhombic	{5,8}	4	(2,7)
	sqc1010		P222	16	orthorhombic	{8,5}	4	(2,7)
	sqc1020		P222	16	orthorhombic	{4,3,8,4,4}	6	(5,6)
	sqc1022		P222	16	orthorhombic	{7,6}	4	(2,7)
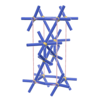
	sqc1023		P222	16	orthorhombic	{3,7}	6	(2,6)
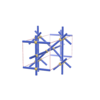
	sqc1027		P222	16	orthorhombic	{6,7}	4	(2,7)
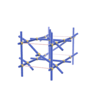
	sqc1042		P222	16	orthorhombic	{3,4,4,4,4}	7	(5,7)
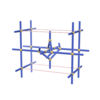
	sqc1047		P222	16	orthorhombic	{4,4,4,4,3}	7	(5,7)
	sqc1053		P222	16	orthorhombic	{4,4,4,3,4}	7	(5,7)
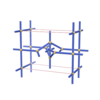
	sqc1058		P222	16	orthorhombic	{4,3,4,4,4}	7	(5,7)
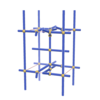
	sqc1081		P222	16	orthorhombic	{4,4,4,3,4}	7	(5,7)
	sqc1083		P222	16	orthorhombic	{10,3}	4	(2,7)
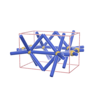
	sqc1084		P222	16	orthorhombic	{10,3}	4	(2,7)
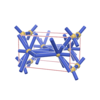
	sqc1085		P222	16	orthorhombic	{3,10}	4	(2,7)
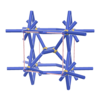
	sqc1086		P222	16	orthorhombic	{8,5}	4	(2,7)
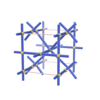
	sqc1097		P222	16	orthorhombic	{4,6,4,4,4}	6	(5,6)
	sqc1098		P222	16	orthorhombic	{6,8,4,4,4}	5	(5,6)
	sqc1105		P222	16	orthorhombic	{4,5}	6	(2,6)
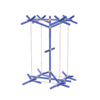
	sqc1106		P222	16	orthorhombic	{6,4,4,4,4}	6	(5,6)
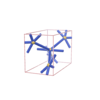
	sqc1111		P222	16	orthorhombic	{5,6}	5	(2,6)
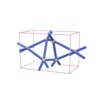
	sqc1112		P222	16	orthorhombic	{5,6}	5	(2,6)
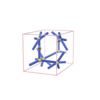
	sqc1113		P222	16	orthorhombic	{5,3}	6	(2,6)
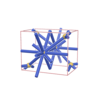
	sqc1130		P222	16	orthorhombic	{4,12}	5	(2,7)
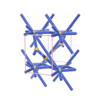
	sqc1180		P222	16	orthorhombic	{3,8}	6	(2,7)
	sqc1181		P222	16	orthorhombic	{3,8}	6	(2,7)
	sqc1189		P222	16	orthorhombic	{4,8,4,4,4}	6	(5,7)
	sqc1193		P222	16	orthorhombic	{4,4,4,8,4}	6	(5,7)
	sqc1260		P222	16	orthorhombic	{4,4,4,4,4}	7	(5,7)
	sqc1274		P222	16	orthorhombic	{3,8}	6	(2,7)
	sqc1294		P222	16	orthorhombic	{4,8,4,4,4}	6	(5,7)
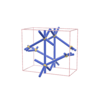
	sqc1307		P222	16	orthorhombic	{4,6}	6	(2,7)
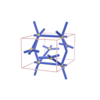
	sqc1308		P222	16	orthorhombic	{4,6}	6	(2,7)
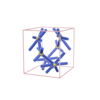
	sqc1328		P222	16	orthorhombic	{6,4}	5	(2,6)
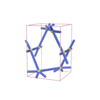
	sqc1364		P222	16	orthorhombic	{5,4}	6	(2,7)
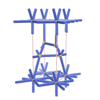
	sqc1448		P222	16	orthorhombic	{10,5}	5	(2,7)
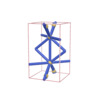
	sqc1472		P222	16	orthorhombic	{3,9}	6	(2,7)
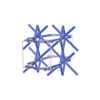
	sqc1480		P222	16	orthorhombic	{4,7}	6	(2,7)
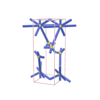
	sqc1481		P222	16	orthorhombic	{4,7}	6	(2,7)
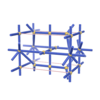
	sqc1516		P222	16	orthorhombic	{4,8,3,4,4,4}	7	(6,7)
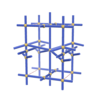
	sqc1519		P222	16	orthorhombic	{4,4,4,4,4,6}	7	(6,7)
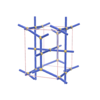
	sqc1525		P222	16	orthorhombic	{4,3,4,4,4,4}	8	(6,7)
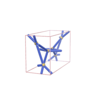
	sqc1526		P222	16	orthorhombic	{5,5}	6	(2,7)
	sqc1527		P222	16	orthorhombic	{5,5}	6	(2,7)
	sqc1528		P222	16	orthorhombic	{4,4,4,6,4,4}	7	(6,7)
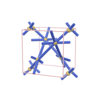
	sqc1535		P222	16	orthorhombic	{6,6}	5	(2,7)
	sqc1536		P222	16	orthorhombic	{6,3}	6	(2,7)
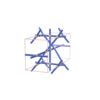
	sqc1537		P222	16	orthorhombic	{3,6}	6	(2,7)
	sqc1546		P222	16	orthorhombic	{3,4,4,4,4,4}	8	(6,7)
	sqc1650		P222	16	orthorhombic	{3,10}	6	(2,8)
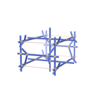
	sqc1674		P222	16	orthorhombic	{4,8}	6	(2,8)
	sqc1711		P222	16	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
	sqc1756		P222	16	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
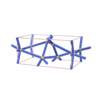
	sqc1778		P222	16	orthorhombic	{3,10}	6	(2,8)
	sqc1880		P222	16	orthorhombic	{5,6}	6	(2,8)
	sqc2218		P222	16	orthorhombic	{4,9}	6	(2,8)
	sqc2222		P222	16	orthorhombic	{5,7}	6	(2,8)
	sqc2230		P222	16	orthorhombic	{3,4,4,4,4,4,4}	9	(7,8)
	sqc2248		P222	16	orthorhombic	{4,3,4,4,4,4,4}	9	(7,8)
	sqc2262		P222	16	orthorhombic	{6,5}	6	(2,8)
	sqc2263		P222	16	orthorhombic	{7,3}	6	(2,8)
	sqc2601		P222	16	orthorhombic	{4,4,4,4,8,4,4}	8	(7,8)
	sqc2709		P222	16	orthorhombic	{3,6}	8	(2,8)
	sqc2784		P222	16	orthorhombic	{5,4}	8	(2,8)
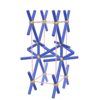
	sqc14561		P222	16	orthorhombic	{3,7}	4	(2,5)
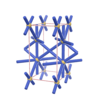
	sqc14566		P222	16	orthorhombic	{3,8}	4	(2,6)
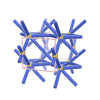
	sqc14570		P222	16	orthorhombic	{9,3}	4	(2,6)
	sqc14572		P222	16	orthorhombic	{7,5}	4	(2,6)
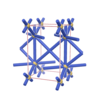
	sqc14574		P222	16	orthorhombic	{3,10}	4	(2,7)
	sqc14576		P222	16	orthorhombic	{5,9}	4	(2,7)