P222

Number	16
Symmetry Class	orthorhombic
Chiral	Y

s-nets

180 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
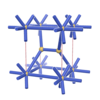
	sqc51		P222	16	orthorhombic	{8,3}	3	(2,4)
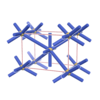
	sqc71		P222	16	orthorhombic	{6,8}	2	(2,4)
	sqc83		P222	16	orthorhombic	{6,10}	2	(2,4)
	sqc98		P222	16	orthorhombic	{4,12}	2	(2,4)
	sqc110		P222	16	orthorhombic	{8,4}	3	(2,5)
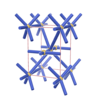
	sqc120		P222	16	orthorhombic	{6,4,6}	3	(3,4)
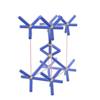
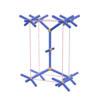
	sqc132		P222	16	orthorhombic	{6,5}	3	(2,4)
	sqc133		P222	16	orthorhombic	{6,3,4}	4	(3,4)
	sqc150		P222	16	orthorhombic	{6,4}	3	(2,5)
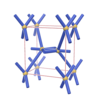
	sqc167		P222	16	orthorhombic	{8,4,4}	3	(3,4)
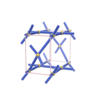
	sqc174		P222	16	orthorhombic	{4,6}	3	(2,4)
	sqc186		P222	16	orthorhombic	{4,4,4}	4	(3,4)
	sqc198		P222	16	orthorhombic	{12,3}	3	(2,5)
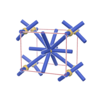
	sqc209		P222	16	orthorhombic	{10,4}	3	(2,5)
	sqc211		P222	16	orthorhombic	{3,12}	3	(2,5)
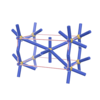
	sqc216		P222	16	orthorhombic	{12,6}	2	(2,5)
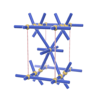
	sqc228		P222	16	orthorhombic	{5,8}	3	(2,5)
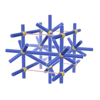
	sqc229		P222	16	orthorhombic	{3,4,8}	4	(3,5)
	sqc243		P222	16	orthorhombic	{4,8,6}	3	(3,5)
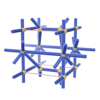
	sqc256		P222	16	orthorhombic	{4,7}	3	(2,4)
	sqc258		P222	16	orthorhombic	{4,8,3}	4	(3,5)
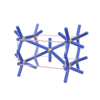
	sqc261		P222	16	orthorhombic	{4,3,8}	4	(3,5)
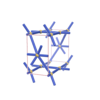
	sqc272		P222	16	orthorhombic	{6,6}	3	(2,5)
	sqc273		P222	16	orthorhombic	{4,6,4}	4	(3,5)
	sqc288		P222	16	orthorhombic	{6,6}	3	(2,5)
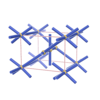
	sqc289		P222	16	orthorhombic	{6,6}	3	(2,5)
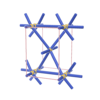
	sqc290		P222	16	orthorhombic	{6,4,4}	4	(3,5)
	sqc291		P222	16	orthorhombic	{4,6,4}	4	(3,5)
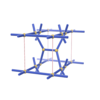
	sqc299		P222	16	orthorhombic	{4,4,3}	5	(3,5)
	sqc302		P222	16	orthorhombic	{4,4,3}	5	(3,5)
	sqc307		P222	16	orthorhombic	{3,4,4}	5	(3,5)
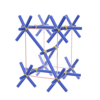
	sqc313		P222	16	orthorhombic	{6,3}	4	(2,5)
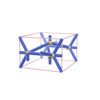
	sqc314		P222	16	orthorhombic	{6,4,4}	4	(3,5)
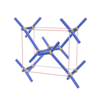
	sqc318		P222	16	orthorhombic	{6,3}	4	(2,5)
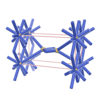
	sqc321		P222	16	orthorhombic	{4,5}	4	(2,5)
	sqc342		P222	16	orthorhombic	{10,5}	3	(2,5)
	sqc346		P222	16	orthorhombic	{6,8}	3	(2,6)
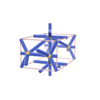
	sqc347		P222	16	orthorhombic	{12,4}	3	(2,6)
	sqc363		P222	16	orthorhombic	{6,8}	3	(2,6)
	sqc364		P222	16	orthorhombic	{8,4,4}	4	(3,6)
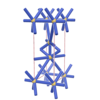
	sqc377		P222	16	orthorhombic	{4,8}	3	(2,6)
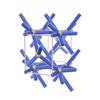
	sqc388		P222	16	orthorhombic	{6,7}	3	(2,5)
	sqc393		P222	16	orthorhombic	{8,4}	3	(2,5)
	sqc405		P222	16	orthorhombic	{8,4,4}	4	(3,6)
	sqc410		P222	16	orthorhombic	{6,7}	3	(2,5)
	sqc411		P222	16	orthorhombic	{6,7}	3	(2,5)
	sqc415		P222	16	orthorhombic	{3,7}	4	(2,5)
	sqc427		P222	16	orthorhombic	{6,3,4,4}	5	(4,5)
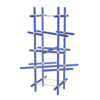
	sqc463		P222	16	orthorhombic	{6,4}	4	(2,6)
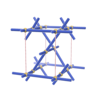
	sqc467		P222	16	orthorhombic	{4,4,4,4}	5	(4,6)
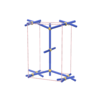
	sqc469		P222	16	orthorhombic	{4,4,4}	5	(3,6)
	sqc471		P222	16	orthorhombic	{4,4,4}	5	(3,6)
	sqc478		P222	16	orthorhombic	{8,4}	3	(2,5)
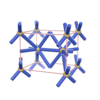
	sqc487		P222	16	orthorhombic	{4,6}	4	(2,6)
	sqc488		P222	16	orthorhombic	{4,8}	3	(2,5)
	sqc491		P222	16	orthorhombic	{6,4}	4	(2,6)
	sqc503		P222	16	orthorhombic	{6,3,4,4}	5	(4,5)
	sqc524		P222	16	orthorhombic	{4,4,4,4}	5	(4,5)
	sqc525		P222	16	orthorhombic	{4,4,4,4}	5	(4,5)
	sqc529		P222	16	orthorhombic	{3,16}	3	(2,6)
	sqc534		P222	16	orthorhombic	{5,12}	3	(2,6)
	sqc538		P222	16	orthorhombic	{6,10}	3	(2,6)
	sqc550		P222	16	orthorhombic	{8,7}	3	(2,6)
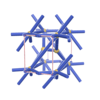
	sqc582		P222	16	orthorhombic	{6,8}	3	(2,6)
	sqc585		P222	16	orthorhombic	{8,3}	4	(2,6)
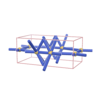
	sqc586		P222	16	orthorhombic	{8,3}	4	(2,6)
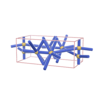
	sqc598		P222	16	orthorhombic	{7,4}	4	(2,6)
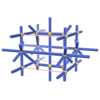
	sqc601		P222	16	orthorhombic	{7,4}	4	(2,6)
	sqc602		P222	16	orthorhombic	{4,3,8,4}	5	(4,6)
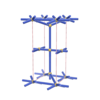
	sqc610		P222	16	orthorhombic	{4,4,6,4}	5	(4,6)
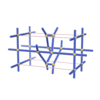
	sqc625		P222	16	orthorhombic	{4,3,4,4}	6	(4,6)
	sqc630		P222	16	orthorhombic	{4,4,3,4}	6	(4,6)
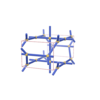
	sqc640		P222	16	orthorhombic	{3,4,4,4}	6	(4,6)
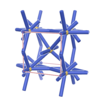
	sqc641		P222	16	orthorhombic	{8,6}	3	(2,6)
	sqc642		P222	16	orthorhombic	{6,4,4,4}	5	(4,6)
	sqc646		P222	16	orthorhombic	{4,6}	5	(2,5)
	sqc655		P222	16	orthorhombic	{4,3,4,4}	6	(4,6)
	sqc657		P222	16	orthorhombic	{4,3,4,4}	6	(4,6)
	sqc661		P222	16	orthorhombic	{4,4,4,3}	6	(4,6)
	sqc664		P222	16	orthorhombic	{3,4,4,4}	6	(4,6)
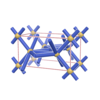
	sqc666		P222	16	orthorhombic	{3,4,4,4}	6	(4,6)
	sqc668		P222	16	orthorhombic	{4,9}	3	(2,5)
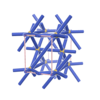
	sqc669		P222	16	orthorhombic	{4,6,8,4}	4	(4,5)
	sqc670		P222	16	orthorhombic	{8,6}	3	(2,6)
	sqc671		P222	16	orthorhombic	{8,3}	4	(2,6)
	sqc674		P222	16	orthorhombic	{3,8}	4	(2,6)
	sqc677		P222	16	orthorhombic	{5,6}	4	(2,6)
	sqc680		P222	16	orthorhombic	{4,8,4,3}	5	(4,6)
	sqc681		P222	16	orthorhombic	{6,4,4,4}	5	(4,6)
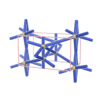
	sqc682		P222	16	orthorhombic	{8,3}	4	(2,6)
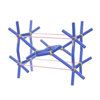
	sqc685		P222	16	orthorhombic	{5,6}	4	(2,6)
	sqc692		P222	16	orthorhombic	{6,5}	4	(2,6)
	sqc715		P222	16	orthorhombic	{3,12}	5	(2,6)
	sqc717		P222	16	orthorhombic	{7,10}	3	(2,6)
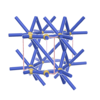
	sqc751		P222	16	orthorhombic	{4,8}	5	(2,6)
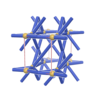
	sqc759		P222	16	orthorhombic	{9,3}	4	(2,6)
	sqc760		P222	16	orthorhombic	{4,8}	4	(2,7)
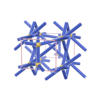
	sqc767		P222	16	orthorhombic	{7,5}	4	(2,6)
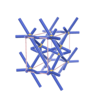
	sqc774		P222	16	orthorhombic	{8,4}	4	(2,7)
	sqc783		P222	16	orthorhombic	{7,5}	4	(2,6)