I213

Number	199
Symmetry Class	cubic
Chiral	Y

s-nets

154 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
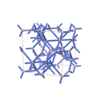
	sqc5416		I213	199	cubic	{6,3}	10	(2,2)
	sqc7073		I213	199	cubic	{9,6}	8	(2,3)
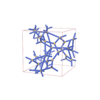
	sqc7279		I213	199	cubic	{6,4,3}	14	(3,3)
	sqc7280		I213	199	cubic	{6,6}	10	(2,3)
	sqc7318		I213	199	cubic	{5}	12	(1,3)
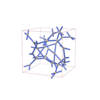
	sqc7346		I213	199	cubic	{4,3}	16	(2,3)
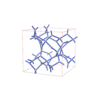
	sqc7389		I213	199	cubic	{3,4}	18	(2,3)
	sqc8584		I213	199	cubic	{3,10}	10	(2,3)
	sqc8970		I213	199	cubic	{4,8}	12	(2,3)
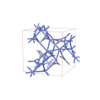
	sqc8976		I213	199	cubic	{8,3,3}	14	(3,3)
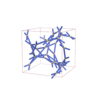
	sqc8995		I213	199	cubic	{3,6}	18	(2,3)
	sqc9015		I213	199	cubic	{4,6}	16	(2,4)
	sqc9049		I213	199	cubic	{6,4}	16	(2,3)
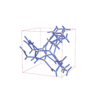
	sqc9060		I213	199	cubic	{4,6,3}	16	(3,3)
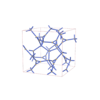
	sqc9065	bch	I213	199	cubic	{6,3,3}	20	(3,3)
	sqc9238		I213	199	cubic	{3,4,3}	22	(3,3)
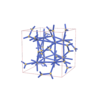
	sqc9990		I213	199	cubic	{9,4}	16	(2,4)
	sqc9991		I213	199	cubic	{9,3,3}	20	(3,4)
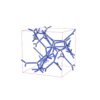
	sqc9992		I213	199	cubic	{9,4}	16	(2,4)
	sqc9993		I213	199	cubic	{9,3,3}	20	(3,4)
	sqc9999		I213	199	cubic	{6,8,3}	14	(3,4)
	sqc10008		I213	199	cubic	{3,8}	18	(2,4)
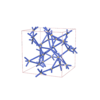
	sqc10011		I213	199	cubic	{3,8}	18	(2,4)
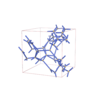
	sqc10019		I213	199	cubic	{5,6}	16	(2,4)
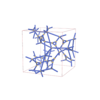
	sqc10021		I213	199	cubic	{4,6,3}	20	(3,4)
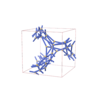
	sqc10022		I213	199	cubic	{3,4,6}	22	(3,4)
	sqc10023		I213	199	cubic	{6,3,6}	20	(3,4)
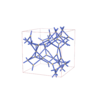
	sqc10027		I213	199	cubic	{3,6}	16	(2,4)
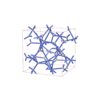
	sqc10034		I213	199	cubic	{3,6,3}	22	(3,4)
	sqc10038		I213	199	cubic	{3,6,3}	22	(3,4)
	sqc10044		I213	199	cubic	{5,4}	18	(2,4)
	sqc10056		I213	199	cubic	{5,4}	18	(2,4)
	sqc10077		I213	199	cubic	{4,3}	24	(2,4)
	sqc10091		I213	199	cubic	{4,4,3}	22	(3,4)
	sqc10741		I213	199	cubic	{12,3,3}	20	(3,5)
	sqc10742		I213	199	cubic	{12,4}	16	(2,5)
	sqc10870		I213	199	cubic	{10,3}	18	(2,4)
	sqc10944		I213	199	cubic	{9,3,6}	20	(3,5)
	sqc10949		I213	199	cubic	{5,9}	16	(2,5)
	sqc10950		I213	199	cubic	{9,4,3}	20	(3,5)
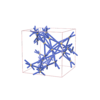
	sqc10987		I213	199	cubic	{4,8}	18	(2,4)
	sqc11020		I213	199	cubic	{6,6}	16	(2,4)
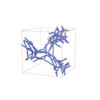
	sqc11023		I213	199	cubic	{5,6}	18	(2,4)
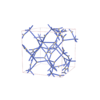
	sqc11037		I213	199	cubic	{4,6,6}	20	(3,5)
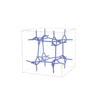
	sqc11080		I213	199	cubic	{3,3,6,3}	26	(4,4)
	sqc11086		I213	199	cubic	{3,5}	24	(2,5)
	sqc11098		I213	199	cubic	{5,3}	24	(2,5)
	sqc11109		I213	199	cubic	{3,5}	24	(2,5)
	sqc11112		I213	199	cubic	{3,5}	24	(2,5)
	sqc11168		I213	199	cubic	{4,4,3,3}	26	(4,4)
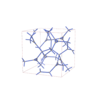
	sqc11221		I213	199	cubic	{4,4,3,3}	26	(4,4)
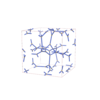
	sqc11223		I213	199	cubic	{3,4,3}	28	(3,5)
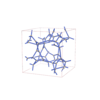
	sqc11228		I213	199	cubic	{3,4,3}	28	(3,5)
	sqc11238		I213	199	cubic	{4,3,4,3}	28	(4,4)
	sqc11599		I213	199	cubic	{12,9,4}	14	(3,5)
	sqc11607		I213	199	cubic	{3,12}	18	(2,5)
	sqc11622		I213	199	cubic	{9,6}	16	(2,5)
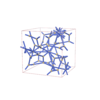
	sqc11624		I213	199	cubic	{9,3,3}	28	(3,5)
	sqc11630		I213	199	cubic	{5,8}	18	(2,5)
	sqc11631		I213	199	cubic	{5,8}	18	(2,5)
	sqc11635		I213	199	cubic	{3,8,3,3}	26	(4,5)
	sqc11639		I213	199	cubic	{7,4}	18	(2,5)
	sqc11644		I213	199	cubic	{7,6}	16	(2,5)
	sqc11651		I213	199	cubic	{4,6,6}	22	(3,5)
	sqc11655		I213	199	cubic	{6,6,3,3}	26	(4,5)
	sqc11656		I213	199	cubic	{6,4,4,3}	26	(4,5)
	sqc11658		I213	199	cubic	{6,4,4,3}	26	(4,5)
	sqc11659		I213	199	cubic	{6,3,3,3}	32	(4,5)
	sqc11660		I213	199	cubic	{6,3,3,3}	32	(4,5)
	sqc11662		I213	199	cubic	{6,3}	24	(2,5)
	sqc11677		I213	199	cubic	{4,6,3,3}	26	(4,5)
	sqc11680		I213	199	cubic	{5,4}	24	(2,5)
	sqc11685		I213	199	cubic	{5,4}	24	(2,5)
	sqc11691		I213	199	cubic	{4,5}	24	(2,5)
	sqc11692		I213	199	cubic	{5,4}	24	(2,5)
	sqc11702		I213	199	cubic	{4,3,3,3}	32	(4,5)
	sqc11711		I213	199	cubic	{4,3,3,3}	32	(4,5)
	sqc11717		I213	199	cubic	{3,3,4,3}	34	(4,5)
	sqc11718		I213	199	cubic	{3,3,4,3}	34	(4,5)
	sqc11725		I213	199	cubic	{3,3,3}	36	(3,5)
	sqc12057		I213	199	cubic	{4,12}	18	(2,5)
	sqc12122		I213	199	cubic	{3,4,9,4}	26	(4,5)
	sqc12126		I213	199	cubic	{3,9,6,4}	26	(4,5)
	sqc12137		I213	199	cubic	{3,8,6,6}	20	(4,5)
	sqc12138		I213	199	cubic	{3,8,3,6}	26	(4,5)
	sqc12142		I213	199	cubic	{8,3,3}	30	(3,5)
	sqc12146		I213	199	cubic	{8,3,3}	30	(3,5)
	sqc12152		I213	199	cubic	{7,3}	24	(2,6)
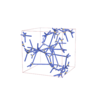
	sqc12158		I213	199	cubic	{3,7}	24	(2,6)
	sqc12170		I213	199	cubic	{4,6}	24	(2,5)
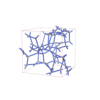
	sqc12189		I213	199	cubic	{6,4,4}	28	(3,5)
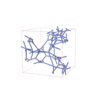
	sqc12190		I213	199	cubic	{4,3,6,3}	32	(4,6)
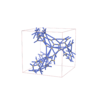
	sqc12191		I213	199	cubic	{6,4,3,3}	32	(4,6)
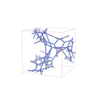
	sqc12192		I213	199	cubic	{6,3,4,3}	32	(4,6)
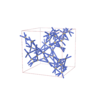
	sqc12196		I213	199	cubic	{4,6}	24	(2,5)
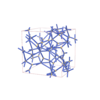
	sqc12207		I213	199	cubic	{3,6,4,6}	28	(4,5)
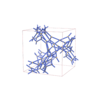
	sqc12211		I213	199	cubic	{3,6,3,4,3}	32	(5,5)
	sqc12228		I213	199	cubic	{5,5}	24	(2,6)
	sqc12239		I213	199	cubic	{4,4,4}	30	(3,5)
	sqc12247		I213	199	cubic	{4,3,3}	36	(3,5)