P4232

Number	208
Symmetry Class	cubic
Chiral	Y

s-nets

428 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
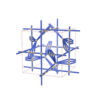
	sqc12493		P4232	208	cubic	{4,4,4,9}	28	(4,5)
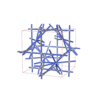
	sqc12498		P4232	208	cubic	{4,4,4,9}	28	(4,5)
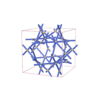
	sqc12499		P4232	208	cubic	{4,9,6,4}	26	(4,5)
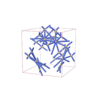
	sqc12500		P4232	208	cubic	{9,4}	28	(2,5)
	sqc12502		P4232	208	cubic	{4,9}	28	(2,5)
	sqc12504		P4232	208	cubic	{4,8,6,3}	26	(4,5)
	sqc12506		P4232	208	cubic	{3,6,4,8}	28	(4,5)
	sqc12507		P4232	208	cubic	{4,4,8,3}	28	(4,5)
	sqc12509		P4232	208	cubic	{6,8,3,6}	26	(4,5)
	sqc12515		P4232	208	cubic	{7,4}	24	(2,5)
	sqc12517		P4232	208	cubic	{7,4}	24	(2,5)
	sqc12519		P4232	208	cubic	{7,4}	24	(2,5)
	sqc12520		P4232	208	cubic	{7,4}	24	(2,5)
	sqc12522		P4232	208	cubic	{6,5}	24	(2,5)
	sqc12524		P4232	208	cubic	{4,6,6,4}	28	(4,5)
	sqc12525		P4232	208	cubic	{4,4,6,6}	28	(4,5)
	sqc12526		P4232	208	cubic	{6,4,4,6}	28	(4,5)
	sqc12529		P4232	208	cubic	{6,4,3,3,3}	38	(5,5)
	sqc12530		P4232	208	cubic	{4,4,6,6}	28	(4,5)
	sqc12531		P4232	208	cubic	{5,6}	24	(2,5)
	sqc12534		P4232	208	cubic	{4,3,6,4}	34	(4,5)
	sqc12535		P4232	208	cubic	{4,3,4,6}	34	(4,5)
	sqc12536		P4232	208	cubic	{3,4,6,4}	34	(4,5)
	sqc12540		P4232	208	cubic	{5,3}	36	(2,5)
	sqc12541		P4232	208	cubic	{3,5}	36	(2,5)
	sqc12544		P4232	208	cubic	{3,5}	36	(2,5)
	sqc12545		P4232	208	cubic	{3,5}	36	(2,5)
	sqc12546		P4232	208	cubic	{5,3}	36	(2,5)
	sqc12549		P4232	208	cubic	{5,3}	36	(2,5)
	sqc12550		P4232	208	cubic	{5,3}	36	(2,5)
	sqc12551		P4232	208	cubic	{5,3}	36	(2,5)
	sqc12552		P4232	208	cubic	{5,3}	36	(2,5)
	sqc12554		P4232	208	cubic	{3,5}	36	(2,5)
	sqc12555		P4232	208	cubic	{4,4,3,4}	34	(4,5)
	sqc12556		P4232	208	cubic	{4,3}	36	(2,5)
	sqc12557		P4232	208	cubic	{3,4}	36	(2,5)
	sqc12558		P4232	208	cubic	{4,3}	36	(2,5)
	sqc12559		P4232	208	cubic	{3,4}	36	(2,5)
	sqc12562		P4232	208	cubic	{4,3}	36	(2,5)
	sqc12563		P4232	208	cubic	{3,4}	36	(2,5)
	sqc12564		P4232	208	cubic	{3,4}	36	(2,5)
	sqc12565		P4232	208	cubic	{3,4}	36	(2,5)
	sqc12567		P4232	208	cubic	{4,4,3,4}	36	(4,5)
	sqc12575		P4232	208	cubic	{3,4,3,4,3}	38	(5,5)
	sqc12576		P4232	208	cubic	{4,3,3,4,3}	38	(5,5)
	sqc12577		P4232	208	cubic	{3,4,4,3,3}	38	(5,5)
	sqc12596		P4232	208	cubic	{12,3}	30	(2,5)
	sqc12617		P4232	208	cubic	{4,4,4,6}	34	(4,6)
	sqc12670		P4232	208	cubic	{8,4}	30	(2,5)
	sqc12671		P4232	208	cubic	{4,8}	30	(2,5)
	sqc12686		P4232	208	cubic	{3,8,3,6,4}	32	(5,5)
	sqc12691		P4232	208	cubic	{4,4,3,3,8}	34	(5,5)
	sqc12720		P4232	208	cubic	{3,4,4,6,6}	32	(5,5)
	sqc12730		P4232	208	cubic	{6,3}	36	(2,6)
	sqc12731		P4232	208	cubic	{6,3}	36	(2,6)
	sqc12733		P4232	208	cubic	{6,3}	36	(2,5)
	sqc12734		P4232	208	cubic	{4,6,4,4,3}	34	(5,5)
	sqc12735		P4232	208	cubic	{4,4,4,6}	34	(4,6)
	sqc12738		P4232	208	cubic	{6,3}	36	(2,5)
	sqc12749		P4232	208	cubic	{3,4,6,4,6}	32	(5,5)
	sqc12759		P4232	208	cubic	{4,4,6,4,3}	34	(5,5)
	sqc12762		P4232	208	cubic	{3,4,3,4,6}	38	(5,5)
	sqc12763		P4232	208	cubic	{4,4,4,6}	34	(4,6)
	sqc12774		P4232	208	cubic	{4,3,6,3,4}	40	(5,5)
	sqc12783		P4232	208	cubic	{4,5}	30	(2,5)
	sqc12824		P4232	208	cubic	{4,4}	36	(2,5)
	sqc12825		P4232	208	cubic	{4,4}	36	(2,5)
	sqc12827		P4232	208	cubic	{4,4}	36	(2,5)
	sqc12828		P4232	208	cubic	{4,4}	36	(2,5)
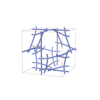
	sqc12834		P4232	208	cubic	{3,4,4,3,6}	38	(5,5)
	sqc12843		P4232	208	cubic	{4,4}	36	(2,6)
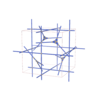
	sqc12846		P4232	208	cubic	{4,4,3,4,3}	40	(5,5)
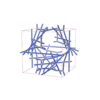
	sqc12887		P4232	208	cubic	{4,3,6,4,4}	40	(5,6)
	sqc12888		P4232	208	cubic	{4,4,3,4,6}	40	(5,6)
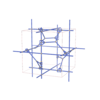
	sqc12889		P4232	208	cubic	{4,3,6,4,4}	40	(5,6)
	sqc12890		P4232	208	cubic	{4,4,3,4,4}	40	(5,6)
	sqc12894		P4232	208	cubic	{3,7}	36	(2,6)
	sqc12895		P4232	208	cubic	{3,7}	36	(2,6)
	sqc12896		P4232	208	cubic	{3,7}	36	(2,6)
	sqc12900		P4232	208	cubic	{7,3}	36	(2,6)
	sqc12901		P4232	208	cubic	{7,3}	36	(2,6)
	sqc12902		P4232	208	cubic	{7,3}	36	(2,6)
	sqc12911		P4232	208	cubic	{6,4,4,3,6}	38	(5,6)
	sqc12912		P4232	208	cubic	{6,4,4,4,3}	38	(5,6)
	sqc12913		P4232	208	cubic	{4,3,4,4,6}	40	(5,6)
	sqc12914		P4232	208	cubic	{6,4,3,4,6}	38	(5,6)
	sqc12917		P4232	208	cubic	{4,4,6,4,3}	38	(5,6)
	sqc12920		P4232	208	cubic	{4,3,6,4,6}	38	(5,6)
	sqc12921		P4232	208	cubic	{3,4,6,4,4}	40	(5,6)
	sqc12922		P4232	208	cubic	{3,4,4,4,6}	40	(5,6)
	sqc12923		P4232	208	cubic	{3,4,4,6,4}	40	(5,6)
	sqc12926		P4232	208	cubic	{5,4}	36	(2,6)
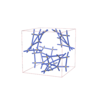
	sqc12927		P4232	208	cubic	{4,5}	36	(2,6)
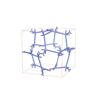
	sqc12931		P4232	208	cubic	{5,3}	36	(2,6)
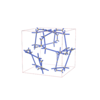
	sqc12932		P4232	208	cubic	{5,3}	36	(2,6)
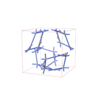
	sqc12933		P4232	208	cubic	{5,3}	36	(2,6)
	sqc12934		P4232	208	cubic	{3,5}	36	(2,6)
	sqc12935		P4232	208	cubic	{5,4}	36	(2,6)
	sqc12936		P4232	208	cubic	{5,4}	36	(2,6)
	sqc12938		P4232	208	cubic	{5,4}	36	(2,6)