h-net: hqc9

Topological data

Orbifold symbol	*246
Transitivity (vertex, edge, ring)	(1,1,1)
Vertex degrees	{4}
2D vertex symbol	{6.6.6.6}
Vertex coordination sequence	[(4, 12, 32, 84, 220, 576, 1508, 3948, 10336, 27060)]
Delaney-Dress Symbol	<9.1:1:1,1,1:6,4>
Dual net	hqc5

Derived s-nets

s-nets with faithful topology

43 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
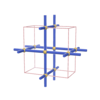
	sqc29	mot	P4/mmm	123	tetragonal	{4,4}	3	(2,2)
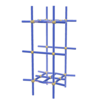
	sqc823		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,7)
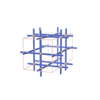
	sqc907		I4/mmm	139	tetragonal	{4,4}	6	(2,3)
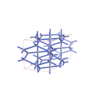
	sqc939		Fmmm	69	orthorhombic	{4,4,4}	6	(3,4)
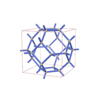
	sqc970	sod	Im-3m	229	cubic	{4}	6	(1,1)
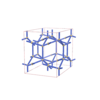
	sqc973		Fmmm	69	orthorhombic	{4,4}	6	(2,3)
	sqc4895		P42/nnm	134	tetragonal	{4,4}	12	(2,4)
	sqc4898		Cmma	67	orthorhombic	{4,4,4,4}	12	(4,7)
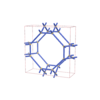
	sqc5264	hbm	P4/mmm	123	tetragonal	{4,4}	12	(2,3)
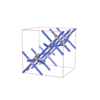
	sqc5341		P42/nnm	134	tetragonal	{4,4}	12	(2,4)
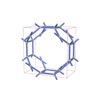
	sqc5513		P4/mmm	123	tetragonal	{4,4}	12	(2,3)
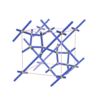
	sqc5543		P42/nnm	134	tetragonal	{4,4}	12	(2,4)
	sqc182	neb	Fddd	70	orthorhombic	{4}	4	(1,2)
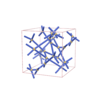
	sqc5111		I4122	98	tetragonal	{4,4}	12	(2,4)
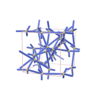
	sqc5236		I4122	98	tetragonal	{4,4,4}	12	(3,4)
	sqc5239		Fddd	70	orthorhombic	{4,4,4}	12	(3,4)
	sqc5257		C2/c	15	monoclinic	{4,4,4,4,4}	12	(5,7)
	sqc5286		Ibca	73	orthorhombic	{4,4}	12	(2,5)
	sqc5288		Ibca	73	orthorhombic	{4,4}	12	(2,5)
	sqc5290		I4122	98	tetragonal	{4,4,4}	12	(3,4)
	sqc5292		C2/c	15	monoclinic	{4,4,4,4}	12	(4,8)
	sqc5298		Fddd	70	orthorhombic	{4,4,4}	12	(3,4)
	sqc5508		Ibca	73	orthorhombic	{4,4}	12	(2,5)
	sqc5515		I4122	98	tetragonal	{4,4}	12	(2,4)
	sqc5518		Ibca	73	orthorhombic	{4,4}	12	(2,5)
	sqc5522		Fddd	70	orthorhombic	{4,4}	12	(2,4)
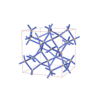
	sqc5561		I41/acd	142	tetragonal	{4,4}	12	(2,2)
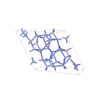
	sqc5579	lcs	Ia-3d	230	cubic	{4}	12	(1,1)
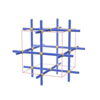
	sqc5580	ict	R-3c	167	rhombohedral	{4}	12	(1,3)
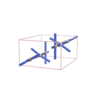
	sqc35	nbo	Im-3m	229	cubic	{4}	3	(1,1)
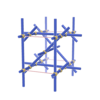
	sqc852		Pnnn	48	orthorhombic	{4,4}	6	(2,4)
	sqc856		P4222	93	tetragonal	{4,4,4}	6	(3,4)
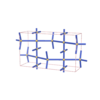
	sqc857		P4222	93	tetragonal	{4,4,4}	6	(3,4)
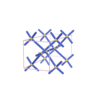
	sqc949		Cmma	67	orthorhombic	{4,4,4}	6	(3,4)
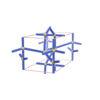
	sqc952		P42/mcm	132	tetragonal	{4,4}	6	(2,3)
	sqc968		P4222	93	tetragonal	{4,4}	6	(2,3)
	sqc969		P42/nnm	134	tetragonal	{4,4}	6	(2,2)
	sqc972		Cmma	67	orthorhombic	{4,4}	6	(2,3)
	sqc974	bbh	Cmma	67	orthorhombic	{4,4}	6	(2,3)
	sqc5287		I41/amd	141	tetragonal	{4,4}	12	(2,4)
	sqc5295		Imma	74	orthorhombic	{4,4,4,4}	12	(4,7)
	sqc5339		I41/amd	141	tetragonal	{4,4}	12	(2,4)
	sqc5509		I41/amd	141	tetragonal	{4,4}	12	(2,4)

s-nets with edge collapse

show / hide

Derived U-tilings

17 records listed.

Image	U-tiling name	PGD Subgroup	Transitivity (Vert,Edge,Face)	Vertex Degree	Vertex Symbol	P net	G net	D net
	UQC3	*246	(1,1,1)	{4}	{6.6.6.6}	sqc970	sqc5579	sqc35
	UQC55	*2224	(2,2,1)	{4,4}	{6.6.6.6}{6.6.6.6}	sqc29	sqc5561	sqc969
	UQC79	*22222a	(3,4,1)	{4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}	sqc4678	sqc5236	sqc857
	UQC80	*22222b	(3,4,1)	{4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}	sqc706	sqc5239	sqc949
	UQC81	*22222b	(3,4,1)	{4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}	sqc939	sqc5298	sqc29
	UQC82	*22222a	(3,4,1)	{4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}	sqc4504	sqc5290	sqc856
	UQC297	*22222a	(2,3,2)	{4,4}	{6.6.6.6}{6.6.6.6}	sqc5264	sqc5111	sqc952
	UQC298	*22222a	(2,3,2)	{4,4}	{6.6.6.6}{6.6.6.6}	sqc5513	sqc5515	sqc968
	UQC299	*22222b	(2,3,2)	{4,4}	{6.6.6.6}{6.6.6.6}	sqc973	sqc5522	sqc972
	UQC300	*22222b	(2,3,2)	{4,4}	{6.6.6.6}{6.6.6.6}	sqc907	sqc182	sqc974
	UQC4	*2626	(2,3,4)	{4,4}	{6.6.6.6}{6.6.6.6}	sqc35	sqc5580	sqc970
	UQC5127	*222222a	(4,7,2)	{4,4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}{6.6....	sqc4898	sqc5292	sqc5295
	UQC5129	*222222a	(4,7,2)	{4,4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}{6.6....	sqc4895	sqc5508	sqc5509
	UQC5130	*222222a	(4,7,2)	{4,4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}{6.6....	sqc5543	sqc5518	sqc5339
	UQC5131	*222222a	(4,7,2)	{4,4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}{6.6....	sqc5341	sqc5288	sqc5287
	UQC5132	*222222b	(4,7,2)	{4,4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}{6.6....	sqc705	sqc5286	sqc852
	UQC5317	*222222a	(5,7,2)	{4,4,4,4,4}	{6.6.6.6}{6.6.6.6}{6.6.6.6}{6.6....	sqc823	sqc5257	sqc4684

Symmetry-lowered hyperbolic tilings

show / hide