Fddd

Number	70
Symmetry Class	orthorhombic
Chiral	N

s-nets

816 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
	sqc182	neb	Fddd	70	orthorhombic	{4}	4	(1,2)
	sqc1801		Fddd	70	orthorhombic	{8}	4	(1,3)
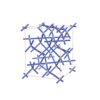
	sqc1878		Fddd	70	orthorhombic	{8}	4	(1,3)
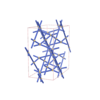
	sqc2045		Fddd	70	orthorhombic	{4,4}	8	(2,3)
	sqc2076		Fddd	70	orthorhombic	{4,4}	8	(2,3)
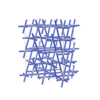
	sqc2309		Fddd	70	orthorhombic	{12,3}	6	(2,4)
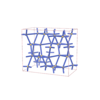
	sqc3364		Fddd	70	orthorhombic	{6,4}	8	(2,3)
	sqc3562		Fddd	70	orthorhombic	{6,4}	8	(2,3)
	sqc3566		Fddd	70	orthorhombic	{6,4}	8	(2,3)
	sqc3571		Fddd	70	orthorhombic	{6,4}	8	(2,3)
	sqc3763		Fddd	70	orthorhombic	{6,4}	8	(2,3)
	sqc4016		Fddd	70	orthorhombic	{3,16}	6	(2,5)
	sqc4773		Fddd	70	orthorhombic	{12,3}	10	(2,5)
	sqc4916		Fddd	70	orthorhombic	{8,4}	8	(2,4)
	sqc4921		Fddd	70	orthorhombic	{8,4}	8	(2,4)
	sqc4962		Fddd	70	orthorhombic	{8,4}	8	(2,4)
	sqc4969		Fddd	70	orthorhombic	{8,4}	8	(2,4)
	sqc4978		Fddd	70	orthorhombic	{8,4}	8	(2,4)
	sqc4988		Fddd	70	orthorhombic	{6,6}	8	(2,4)
	sqc5020		Fddd	70	orthorhombic	{8,4}	8	(2,4)
	sqc5067		Fddd	70	orthorhombic	{8,4}	8	(2,4)
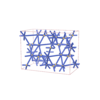
	sqc5095		Fddd	70	orthorhombic	{6}	8	(1,4)
	sqc5141		Fddd	70	orthorhombic	{8,4}	8	(2,4)
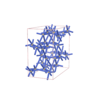
	sqc5142		Fddd	70	orthorhombic	{8,4}	8	(2,4)
	sqc5144		Fddd	70	orthorhombic	{6}	8	(1,4)
	sqc5162		Fddd	70	orthorhombic	{6,6}	8	(2,4)
	sqc5165		Fddd	70	orthorhombic	{6,6}	8	(2,4)
	sqc5166		Fddd	70	orthorhombic	{6,6}	8	(2,4)
	sqc5173		Fddd	70	orthorhombic	{6,6}	8	(2,4)
	sqc5174		Fddd	70	orthorhombic	{6,6}	8	(2,4)
	sqc5175		Fddd	70	orthorhombic	{3,6}	12	(2,4)
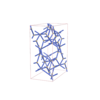
	sqc5190		Fddd	70	orthorhombic	{3,6}	12	(2,4)
	sqc5192		Fddd	70	orthorhombic	{3,6}	12	(2,4)
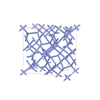
	sqc5193		Fddd	70	orthorhombic	{3,6}	12	(2,4)
	sqc5239		Fddd	70	orthorhombic	{4,4,4}	12	(3,4)
	sqc5273		Fddd	70	orthorhombic	{4,4}	12	(2,4)
	sqc5277		Fddd	70	orthorhombic	{4,4}	12	(2,4)
	sqc5278		Fddd	70	orthorhombic	{4,4}	12	(2,4)
	sqc5282		Fddd	70	orthorhombic	{4,4}	12	(2,4)
	sqc5283		Fddd	70	orthorhombic	{4,4}	12	(2,4)
	sqc5298		Fddd	70	orthorhombic	{4,4,4}	12	(3,4)
	sqc5331		Fddd	70	orthorhombic	{3,6}	12	(2,4)
	sqc5332		Fddd	70	orthorhombic	{3,6}	12	(2,4)
	sqc5354		Fddd	70	orthorhombic	{8,4}	8	(2,4)
	sqc5361		Fddd	70	orthorhombic	{6,6}	8	(2,4)
	sqc5368		Fddd	70	orthorhombic	{3,6}	12	(2,4)
	sqc5370		Fddd	70	orthorhombic	{3,6}	12	(2,4)
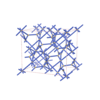
	sqc5371		Fddd	70	orthorhombic	{3,6}	12	(2,4)
	sqc5379		Fddd	70	orthorhombic	{3,6}	12	(2,4)
	sqc5522		Fddd	70	orthorhombic	{4,4}	12	(2,4)
	sqc6342		Fddd	70	orthorhombic	{10,4}	8	(2,4)
	sqc6343		Fddd	70	orthorhombic	{10,4}	8	(2,4)
	sqc6345		Fddd	70	orthorhombic	{10,4}	8	(2,4)
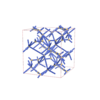
	sqc6348		Fddd	70	orthorhombic	{8,6}	8	(2,5)
	sqc6349		Fddd	70	orthorhombic	{8,3}	12	(2,5)
	sqc6358		Fddd	70	orthorhombic	{3,8}	12	(2,5)
	sqc6387		Fddd	70	orthorhombic	{10,4}	8	(2,4)
	sqc6407		Fddd	70	orthorhombic	{8,6}	8	(2,5)
	sqc6466		Fddd	70	orthorhombic	{10,4}	8	(2,4)
	sqc6517		Fddd	70	orthorhombic	{8,6}	8	(2,5)
	sqc6518		Fddd	70	orthorhombic	{8,6}	8	(2,5)
	sqc6519		Fddd	70	orthorhombic	{3,8}	12	(2,5)
	sqc6520		Fddd	70	orthorhombic	{3,8}	12	(2,5)
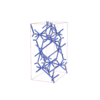
	sqc6521		Fddd	70	orthorhombic	{3,8}	12	(2,5)
	sqc6528		Fddd	70	orthorhombic	{3,8}	12	(2,5)
	sqc6541		Fddd	70	orthorhombic	{8,6}	8	(2,5)
	sqc6543		Fddd	70	orthorhombic	{4,6}	12	(2,5)
	sqc6560		Fddd	70	orthorhombic	{4,6}	12	(2,5)
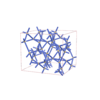
	sqc6561		Fddd	70	orthorhombic	{4,6}	12	(2,5)
	sqc6563		Fddd	70	orthorhombic	{6,4}	12	(2,5)
	sqc6574		Fddd	70	orthorhombic	{5,4}	12	(2,4)
	sqc6579		Fddd	70	orthorhombic	{5,4}	12	(2,4)
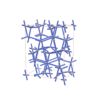
	sqc6585		Fddd	70	orthorhombic	{5,4}	12	(2,4)
	sqc6586		Fddd	70	orthorhombic	{5,4}	12	(2,4)
	sqc6607		Fddd	70	orthorhombic	{4,6,4}	12	(3,4)
	sqc6643		Fddd	70	orthorhombic	{4,6,4}	12	(3,4)
	sqc6648		Fddd	70	orthorhombic	{4,6,4}	12	(3,4)
	sqc6659		Fddd	70	orthorhombic	{4,3,4}	16	(3,4)
	sqc6660		Fddd	70	orthorhombic	{4,3,4}	16	(3,4)
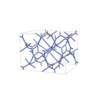
	sqc6661		Fddd	70	orthorhombic	{4,3,4}	16	(3,4)
	sqc6677		Fddd	70	orthorhombic	{8,3}	12	(2,5)
	sqc6693		Fddd	70	orthorhombic	{6,4}	12	(2,5)
	sqc6694		Fddd	70	orthorhombic	{4,6}	12	(2,5)
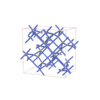
	sqc6703		Fddd	70	orthorhombic	{5,4}	12	(2,4)
	sqc6710		Fddd	70	orthorhombic	{4,3,4}	16	(3,4)
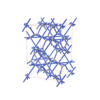
	sqc6720		Fddd	70	orthorhombic	{8,3}	12	(2,5)
	sqc6727		Fddd	70	orthorhombic	{3,8}	12	(2,5)
	sqc6728		Fddd	70	orthorhombic	{3,8}	12	(2,5)
	sqc6734		Fddd	70	orthorhombic	{4,6}	12	(2,5)
	sqc6735		Fddd	70	orthorhombic	{4,6}	12	(2,5)
	sqc6743		Fddd	70	orthorhombic	{4,6}	12	(2,5)
	sqc6746		Fddd	70	orthorhombic	{4,6}	12	(2,5)
	sqc6793		Fddd	70	orthorhombic	{4,6,4}	12	(3,4)
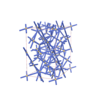
	sqc6794		Fddd	70	orthorhombic	{4,6,4}	12	(3,4)
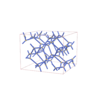
	sqc6924		Fddd	70	orthorhombic	{3,4}	16	(2,5)
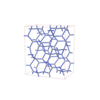
	sqc6949		Fddd	70	orthorhombic	{3,4}	16	(2,5)
	sqc6956		Fddd	70	orthorhombic	{3,4}	16	(2,5)
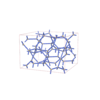
	sqc6957		Fddd	70	orthorhombic	{3,4}	16	(2,5)
	sqc6959		Fddd	70	orthorhombic	{3,4}	16	(2,5)
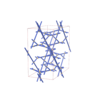
	sqc6961		Fddd	70	orthorhombic	{4,3,4}	16	(3,4)