Pmmm
| Number | 47 |
| Symmetry Class | orthorhombic |
| Chiral | N |
s-nets
833 records listed.
| Image |
s-net name |
Other names |
Space group |
Space group number |
Symmetry class |
Vertex degree(s) |
Vertices per primitive unit cell |
Transitivity (Vertex, Edge) |

|
sqc2
|
|
Pmmm |
47 |
orthorhombic |
{8} |
1 |
(1,3) |

|
sqc9
|
|
Pmmm |
47 |
orthorhombic |
{4,6} |
2 |
(2,4) |

|
sqc10
|
fsg
|
Pmmm |
47 |
orthorhombic |
{4,6} |
2 |
(2,4) |

|
sqc16
|
|
Pmmm |
47 |
orthorhombic |
{4,8} |
2 |
(2,4) |

|
sqc17
|
|
Pmmm |
47 |
orthorhombic |
{8,4} |
2 |
(2,4) |

|
sqc18
|
|
Pmmm |
47 |
orthorhombic |
{8,4} |
2 |
(2,4) |

|
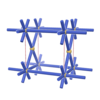
sqc20
|
|
Pmmm |
47 |
orthorhombic |
{4,8} |
2 |
(2,5) |
|
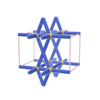
sqc21
|
|
Pmmm |
47 |
orthorhombic |
{8,4} |
2 |
(2,3) |
|
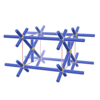
sqc24
|
|
Pmmm |
47 |
orthorhombic |
{6} |
2 |
(1,4) |
|
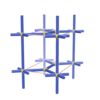
sqc25
|
|
Pmmm |
47 |
orthorhombic |
{6,6} |
2 |
(2,3) |
|
sqc27
|
|
Pmmm |
47 |
orthorhombic |
{6,3} |
3 |
(2,3) |

|
sqc28
|
|
Pmmm |
47 |
orthorhombic |
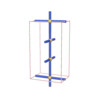
{4,4,4} |
3 |
(3,4) |
|
sqc30
|
cdz
|
Pmmm |
47 |
orthorhombic |
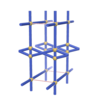
{4,4} |
3 |
(2,4) |
|
sqc31
|
|
Pmmm |
47 |
orthorhombic |
{4,4} |
3 |
(2,4) |

|
sqc40
|
|
Pmmm |
47 |
orthorhombic |
{10,4} |
2 |
(2,5) |

|
sqc41
|
|
Pmmm |
47 |
orthorhombic |
{4,10} |
2 |
(2,5) |

|
sqc42
|
|
Pmmm |
47 |
orthorhombic |
{10,4} |
2 |
(2,3) |

|
sqc45
|
|
Pmmm |
47 |
orthorhombic |
{8,6} |
2 |
(2,4) |

|
sqc46
|
seb
|
Pmmm |
47 |
orthorhombic |
{6,8} |
2 |
(2,4) |

|
sqc47
|
|
Pmmm |
47 |
orthorhombic |
{6,8} |
2 |
(2,4) |

|
sqc48
|
|
Pmmm |
47 |
orthorhombic |
{3,8} |
3 |
(2,4) |

|
sqc50
|
|
Pmmm |
47 |
orthorhombic |
{3,8} |
3 |
(2,4) |

|
sqc52
|
|
Pmmm |
47 |
orthorhombic |
{6,8} |
2 |
(2,5) |

|
sqc53
|
|
Pmmm |
47 |
orthorhombic |
{4,4,6} |
3 |
(3,5) |

|
sqc54
|
|
Pmmm |
47 |
orthorhombic |
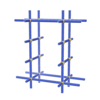
{4,4,6} |
3 |
(3,5) |
|
sqc55
|
|
Pmmm |
47 |
orthorhombic |
{6,4} |
3 |
(2,5) |

|
sqc57
|
|
Pmmm |
47 |
orthorhombic |
{4,6} |
3 |
(2,5) |

|
sqc62
|
|
Pmmm |
47 |
orthorhombic |
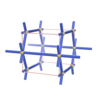
{4,4,6} |
3 |
(3,5) |
|
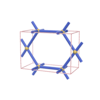
sqc63
|
|
Pmmm |
47 |
orthorhombic |
{6,4} |
3 |
(2,4) |
|
sqc65
|
|
Pmmm |
47 |
orthorhombic |
{4,5} |
3 |
(2,3) |

|
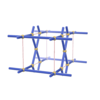
sqc67
|
|
Pmmm |
47 |
orthorhombic |
{4,4,6} |
3 |
(3,3) |
|
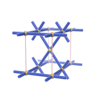
sqc69
|
|
Pmmm |
47 |
orthorhombic |
{4,4,3} |
4 |
(3,3) |
|
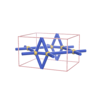
sqc72
|
|
Pmmm |
47 |
orthorhombic |
{4,4,6} |
3 |
(3,3) |
|
sqc73
|
|
Pmmm |
47 |
orthorhombic |
{5,4} |
3 |
(2,3) |

|
sqc75
|
|
Pmmm |
47 |
orthorhombic |
{10,3} |
3 |
(2,4) |
|
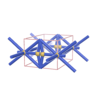
sqc76
|
|
Pmmm |
47 |
orthorhombic |
{4,8} |
3 |
(2,5) |
|
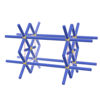
sqc77
|
|
Pmmm |
47 |
orthorhombic |
{10,6} |
2 |
(2,4) |
|
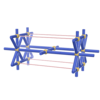
sqc78
|
|
Pmmm |
47 |
orthorhombic |
{4,4,8} |
3 |
(3,5) |

|
sqc79
|
|
Pmmm |
47 |
orthorhombic |
{4,12} |
2 |
(2,5) |

|
sqc80
|
|
Pmmm |
47 |
orthorhombic |
{12,4} |
2 |
(2,4) |
|
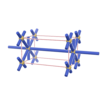
sqc81
|
|
Pmmm |
47 |
orthorhombic |
{4,12} |
2 |
(2,4) |
|
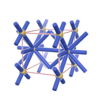
sqc82
|
|
Pmmm |
47 |
orthorhombic |
{4,12} |
2 |
(2,4) |

|
sqc84
|
|
Pmmm |
47 |
orthorhombic |
{6,10} |
2 |
(2,4) |

|
sqc85
|
|
Pmmm |
47 |
orthorhombic |
{6,10} |
2 |
(2,4) |

|
sqc86
|
|
Pmmm |
47 |
orthorhombic |
{10,6} |
2 |
(2,4) |

|
sqc87
|
|
Pmmm |
47 |
orthorhombic |
{10,3} |
3 |
(2,4) |

|
sqc88
|
|
Pmmm |
47 |
orthorhombic |
{8,4,4} |
3 |
(3,5) |
|
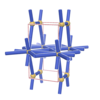
sqc89
|
|
Pmmm |
47 |
orthorhombic |
{3,10} |
3 |
(2,4) |

|
sqc91
|
|
Pmmm |
47 |
orthorhombic |
{8,4,4} |
3 |
(3,5) |

|
sqc92
|
|
Pmmm |
47 |
orthorhombic |
{8,4} |
3 |
(2,5) |
|
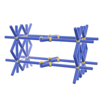
sqc93
|
|
Pmmm |
47 |
orthorhombic |
{8,4} |
3 |
(2,5) |

|
sqc99
|
|
Pmmm |
47 |
orthorhombic |
{10,6} |
2 |
(2,5) |

|
sqc102
|
|
Pmmm |
47 |
orthorhombic |
{10,3} |
3 |
(2,5) |
|
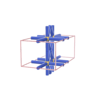
sqc104
|
|
Pmmm |
47 |
orthorhombic |
{8} |
2 |
(1,5) |

|
sqc105
|
|
Pmmm |
47 |
orthorhombic |
{8,8} |
2 |
(2,5) |

|
sqc107
|
|
Pmmm |
47 |
orthorhombic |
{4,8} |
3 |
(2,5) |

|
sqc109
|
|
Pmmm |
47 |
orthorhombic |
{4,8} |
3 |
(2,5) |

|
sqc112
|
|
Pmmm |
47 |
orthorhombic |
{4,6} |
3 |
(2,5) |

|
sqc114
|
|
Pmmm |
47 |
orthorhombic |
{6,4} |
3 |
(2,5) |
|
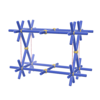
sqc115
|
|
Pmmm |
47 |
orthorhombic |
{8,4,4} |
3 |
(3,4) |

|
sqc116
|
|
Pmmm |
47 |
orthorhombic |
{8,4,4} |
3 |
(3,4) |

|
sqc118
|
|
Pmmm |
47 |
orthorhombic |
{6,6,4} |
3 |
(3,4) |
|
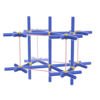
sqc119
|
|
Pmmm |
47 |
orthorhombic |
{6,6,4} |
3 |
(3,4) |
|
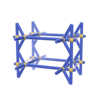
sqc122
|
|
Pmmm |
47 |
orthorhombic |
{4,6} |
3 |
(2,5) |

|
sqc123
|
|
Pmmm |
47 |
orthorhombic |
{4,6} |
3 |
(2,4) |

|
sqc126
|
|
Pmmm |
47 |
orthorhombic |
{5,6} |
3 |
(2,4) |

|
sqc127
|
|
Pmmm |
47 |
orthorhombic |
{6,5} |
3 |
(2,4) |

|
sqc128
|
|
Pmmm |
47 |
orthorhombic |
{6,5} |
3 |
(2,4) |

|
sqc129
|
|
Pmmm |
47 |
orthorhombic |
{3,4,6} |
4 |
(3,4) |
|
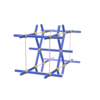
sqc130
|
|
Pmmm |
47 |
orthorhombic |
{3,4,6} |
4 |
(3,4) |

|
sqc131
|
|
Pmmm |
47 |
orthorhombic |
{4,3,6} |
4 |
(3,4) |
|
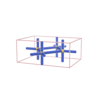
sqc134
|
btv
|
Pmmm |
47 |
orthorhombic |
{5,6} |
3 |
(2,4) |
|
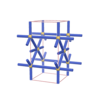
sqc136
|
|
Pmmm |
47 |
orthorhombic |
{5,6} |
3 |
(2,4) |
|
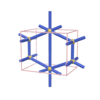
sqc137
|
|
Pmmm |
47 |
orthorhombic |
{5,6} |
3 |
(2,4) |

|
sqc138
|
|
Pmmm |
47 |
orthorhombic |
{5,3} |
4 |
(2,4) |

|
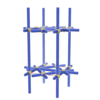
sqc139
|
|
Pmmm |
47 |
orthorhombic |
{8,4,4} |
3 |
(3,5) |
|
sqc140
|
|
Pmmm |
47 |
orthorhombic |
{4,8,4} |
3 |
(3,4) |

|
sqc142
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4,4} |
4 |
(4,5) |

|
sqc143
|
|
Pmmm |
47 |
orthorhombic |
{6,4,6} |
3 |
(3,4) |
|
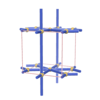
sqc144
|
|
Pmmm |
47 |
orthorhombic |
{3,4,6} |
4 |
(3,4) |

|
sqc146
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4} |
4 |
(3,5) |

|
sqc147
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4} |
4 |
(3,5) |

|
sqc148
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4} |
4 |
(3,5) |

|
sqc149
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4} |
4 |
(3,5) |

|
sqc151
|
|
Pmmm |
47 |
orthorhombic |
{6,4} |
3 |
(2,5) |

|
sqc152
|
|
Pmmm |
47 |
orthorhombic |
{6,4} |
3 |
(2,5) |
|
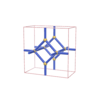
sqc153
|
|
Pmmm |
47 |
orthorhombic |
{5,3} |
4 |
(2,4) |

|
sqc154
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4} |
4 |
(3,5) |
|
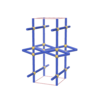
sqc156
|
|
Pmmm |
47 |
orthorhombic |
{4,4} |
4 |
(2,5) |

|
sqc158
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4} |
4 |
(3,5) |
|
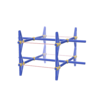
sqc159
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4} |
4 |
(3,5) |

|
sqc160
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4} |
4 |
(3,4) |
|
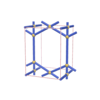
sqc161
|
|
Pmmm |
47 |
orthorhombic |
{4,4,4} |
4 |
(3,4) |
|
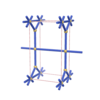
sqc162
|
|
Pmmm |
47 |
orthorhombic |
{3,4,6} |
4 |
(3,4) |
|
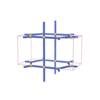
sqc163
|
|
Pmmm |
47 |
orthorhombic |
{3,3,4} |
5 |
(3,4) |

|
sqc164
|
|
Pmmm |
47 |
orthorhombic |
{3,3,4} |
5 |
(3,4) |

|
sqc171
|
|
Pmmm |
47 |
orthorhombic |
{6,6,4} |
3 |
(3,4) |
|
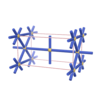
sqc172
|
|
Pmmm |
47 |
orthorhombic |
{6,6,4} |
3 |
(3,4) |
|
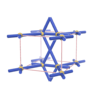
sqc175
|
|
Pmmm |
47 |
orthorhombic |
{4,6} |
3 |
(2,4) |
|
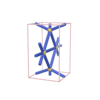
sqc177
|
|
Pmmm |
47 |
orthorhombic |
{5,6} |
3 |
(2,4) |



































































































