I41/acd

Number	142
Symmetry Class	tetragonal
Chiral	N

s-nets

601 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
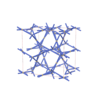
	sqc12401		I41/acd	142	tetragonal	{6,6,4}	24	(3,4)
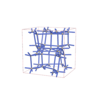
	sqc12402		I41/acd	142	tetragonal	{4,6}	24	(2,4)
	sqc12403		I41/acd	142	tetragonal	{5,6}	24	(2,5)
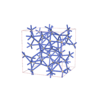
	sqc12404		I41/acd	142	tetragonal	{6,5}	24	(2,5)
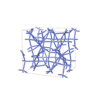
	sqc12405		I41/acd	142	tetragonal	{6,4,4}	28	(3,5)
	sqc12406		I41/acd	142	tetragonal	{4,6,4}	28	(3,5)
	sqc12407		I41/acd	142	tetragonal	{4,6,4}	28	(3,5)
	sqc12408		I41/acd	142	tetragonal	{6,4,4}	28	(3,5)
	sqc12409		I41/acd	142	tetragonal	{3,5}	32	(2,5)
	sqc12410		I41/acd	142	tetragonal	{5,3}	32	(2,5)
	sqc12411		I41/acd	142	tetragonal	{5,3}	32	(2,5)
	sqc12412		I41/acd	142	tetragonal	{3,5}	32	(2,5)
	sqc12413		I41/acd	142	tetragonal	{3,5}	32	(2,5)
	sqc12414		I41/acd	142	tetragonal	{3,5}	32	(2,5)
	sqc12435		I41/acd	142	tetragonal	{5,3}	32	(2,5)
	sqc12436		I41/acd	142	tetragonal	{5,3}	32	(2,5)
	sqc12437		I41/acd	142	tetragonal	{3,5}	32	(2,5)
	sqc12438		I41/acd	142	tetragonal	{3,5}	32	(2,5)
	sqc12439		I41/acd	142	tetragonal	{3,5}	32	(2,5)
	sqc12440		I41/acd	142	tetragonal	{3,5}	32	(2,5)
	sqc12441		I41/acd	142	tetragonal	{4,4}	32	(2,5)
	sqc12442		I41/acd	142	tetragonal	{4,3,4}	36	(3,5)
	sqc12443		I41/acd	142	tetragonal	{3,4,4}	36	(3,5)
	sqc12444		I41/acd	142	tetragonal	{4,4}	32	(2,5)
	sqc12449		I41/acd	142	tetragonal	{4,4}	32	(2,5)
	sqc12450		I41/acd	142	tetragonal	{4,4}	32	(2,5)
	sqc12455		I41/acd	142	tetragonal	{3,4,4}	36	(3,5)
	sqc12456		I41/acd	142	tetragonal	{4,3,4,4}	36	(4,4)
	sqc12457		I41/acd	142	tetragonal	{4,3,4,4}	36	(4,4)
	sqc12458		I41/acd	142	tetragonal	{4,4}	32	(2,5)
	sqc12459		I41/acd	142	tetragonal	{4,4}	32	(2,4)
	sqc12460		I41/acd	142	tetragonal	{3,4,4}	36	(3,5)
	sqc12461		I41/acd	142	tetragonal	{3,4,4}	36	(3,5)
	sqc12462		I41/acd	142	tetragonal	{3,4,4}	36	(3,5)
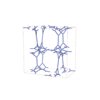
	sqc12463		I41/acd	142	tetragonal	{3,3,4}	40	(3,5)
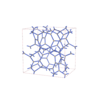
	sqc12464		I41/acd	142	tetragonal	{4,3,3}	40	(3,5)
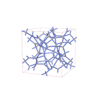
	sqc12465		I41/acd	142	tetragonal	{4,3,4}	36	(3,5)
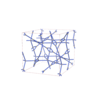
	sqc12466		I41/acd	142	tetragonal	{3,4,4}	36	(3,5)
	sqc12467		I41/acd	142	tetragonal	{3,4,4}	36	(3,5)
	sqc12468		I41/acd	142	tetragonal	{3,4,4}	36	(3,5)
	sqc12469		I41/acd	142	tetragonal	{4,3,4}	36	(3,5)
	sqc12470		I41/acd	142	tetragonal	{4,3,4}	36	(3,5)
	sqc12471		I41/acd	142	tetragonal	{4,3,3}	40	(3,4)
	sqc12472		I41/acd	142	tetragonal	{4,3,3}	40	(3,4)
	sqc12473		I41/acd	142	tetragonal	{4,3,3}	40	(3,4)
	sqc12579		I41/acd	142	tetragonal	{16,6,4}	20	(3,5)
	sqc12580		I41/acd	142	tetragonal	{16,6,4}	20	(3,5)
	sqc12581		I41/acd	142	tetragonal	{12,3,3}	36	(3,5)
	sqc12582		I41/acd	142	tetragonal	{12,3,3}	36	(3,5)
	sqc12583		I41/acd	142	tetragonal	{8,4,3}	36	(3,6)
	sqc12584		I41/acd	142	tetragonal	{8,4,3}	36	(3,6)
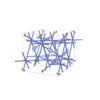
	sqc12585		I41/acd	142	tetragonal	{3,4,8}	36	(3,6)
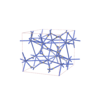
	sqc12586		I41/acd	142	tetragonal	{3,4,8}	36	(3,6)
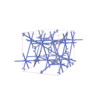
	sqc12587		I41/acd	142	tetragonal	{4,3,8}	36	(3,6)
	sqc12588		I41/acd	142	tetragonal	{4,3,8}	36	(3,6)
	sqc12593		I41/acd	142	tetragonal	{10,4}	24	(2,5)
	sqc12600		I41/acd	142	tetragonal	{7,4}	24	(2,5)
	sqc12601		I41/acd	142	tetragonal	{6,6}	24	(2,5)
	sqc12602		I41/acd	142	tetragonal	{3,6}	32	(2,5)
	sqc12603		I41/acd	142	tetragonal	{3,6}	32	(2,6)
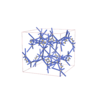
	sqc12604		I41/acd	142	tetragonal	{6,3}	32	(2,6)
	sqc12607		I41/acd	142	tetragonal	{3,6}	32	(2,5)
	sqc12608		I41/acd	142	tetragonal	{3,6}	32	(2,5)
	sqc12609		I41/acd	142	tetragonal	{5,4}	32	(2,6)
	sqc12610		I41/acd	142	tetragonal	{5,4}	32	(2,5)
	sqc12612		I41/acd	142	tetragonal	{4,5}	32	(2,5)
	sqc12613		I41/acd	142	tetragonal	{4,4,4,4}	36	(4,5)
	sqc12614		I41/acd	142	tetragonal	{4,6,3,4}	36	(4,5)
	sqc12620		I41/acd	142	tetragonal	{4,4,4,4}	36	(4,5)
	sqc12621		I41/acd	142	tetragonal	{4,3,3,4}	44	(4,5)
	sqc12622		I41/acd	142	tetragonal	{4,3,3,4}	44	(4,5)
	sqc12624		I41/acd	142	tetragonal	{5,8}	24	(2,5)
	sqc12625		I41/acd	142	tetragonal	{10,4}	24	(2,5)
	sqc12626		I41/acd	142	tetragonal	{7,4}	24	(2,5)
	sqc12628		I41/acd	142	tetragonal	{6,3,3}	40	(3,5)
	sqc12629		I41/acd	142	tetragonal	{5,8}	24	(2,5)
	sqc12630		I41/acd	142	tetragonal	{5,4}	32	(2,5)
	sqc12632		I41/acd	142	tetragonal	{5,4}	32	(2,5)
	sqc12636		I41/acd	142	tetragonal	{8,12,4}	20	(3,5)
	sqc12637		I41/acd	142	tetragonal	{6,3,3}	40	(3,5)
	sqc12638		I41/acd	142	tetragonal	{6,3,4,4}	36	(4,5)
	sqc12639		I41/acd	142	tetragonal	{6,3,3}	40	(3,5)
	sqc12640		I41/acd	142	tetragonal	{8,3,8}	28	(3,5)
	sqc12641		I41/acd	142	tetragonal	{8,6,8}	20	(3,5)
	sqc12643		I41/acd	142	tetragonal	{4,12,4}	28	(3,5)
	sqc12644		I41/acd	142	tetragonal	{8,12,4}	20	(3,5)
	sqc12645		I41/acd	142	tetragonal	{4,12,4}	28	(3,5)
	sqc12666		I41/acd	142	tetragonal	{4,6,8}	28	(3,5)
	sqc12667		I41/acd	142	tetragonal	{4,6,8}	28	(3,5)
	sqc12682		I41/acd	142	tetragonal	{8,3,8}	28	(3,5)
	sqc12700		I41/acd	142	tetragonal	{7,4}	24	(2,5)
	sqc12701		I41/acd	142	tetragonal	{7,4}	24	(2,5)
	sqc12703		I41/acd	142	tetragonal	{6,6}	24	(2,5)
	sqc12704		I41/acd	142	tetragonal	{6,3}	32	(2,6)
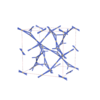
	sqc12713		I41/acd	142	tetragonal	{4,6,4}	32	(3,5)
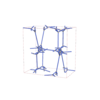
	sqc12718		I41/acd	142	tetragonal	{3,6}	32	(2,6)
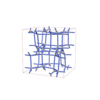
	sqc12719		I41/acd	142	tetragonal	{3,6}	32	(2,5)
	sqc12721		I41/acd	142	tetragonal	{4,6,4}	32	(3,5)
	sqc12726		I41/acd	142	tetragonal	{6,3,4,4}	36	(4,5)
	sqc12729		I41/acd	142	tetragonal	{6,3,3}	40	(3,5)