Cmmm

Number	65
Symmetry Class	orthorhombic
Chiral	N

s-nets

120 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
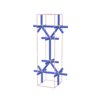
	sqc32		Cmmm	65	orthorhombic	{8,4}	2	(2,4)
	sqc49	svk	Cmmm	65	orthorhombic	{7}	2	(1,4)
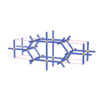
	sqc58		Cmmm	65	orthorhombic	{4,10}	2	(2,3)
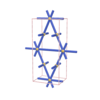
	sqc64		Cmmm	65	orthorhombic	{5,4}	3	(2,4)
	sqc66		Cmmm	65	orthorhombic	{4,6}	3	(2,3)
	sqc96		Cmmm	65	orthorhombic	{4,12}	2	(2,4)
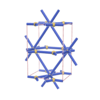
	sqc97		Cmmm	65	orthorhombic	{10,3}	3	(2,4)
	sqc101		Cmmm	65	orthorhombic	{3,10}	3	(2,4)
	sqc103		Cmmm	65	orthorhombic	{8,4}	3	(2,5)
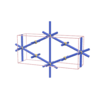
	sqc108		Cmmm	65	orthorhombic	{4,8}	3	(2,4)
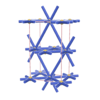
	sqc113		Cmmm	65	orthorhombic	{6,10}	2	(2,4)
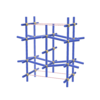
	sqc121		Cmmm	65	orthorhombic	{6,4}	3	(2,5)
	sqc124		Cmmm	65	orthorhombic	{6,4}	3	(2,3)
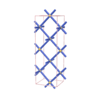
	sqc125		Cmmm	65	orthorhombic	{6,4}	3	(2,3)
	sqc135		Cmmm	65	orthorhombic	{5,6}	3	(2,5)
	sqc212		Cmmm	65	orthorhombic	{3,12}	3	(2,5)
	sqc213		Cmmm	65	orthorhombic	{12,3}	3	(2,5)
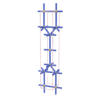
	sqc215		Cmmm	65	orthorhombic	{10,4}	3	(2,5)
	sqc231		Cmmm	65	orthorhombic	{7,4}	3	(2,5)
	sqc244		Cmmm	65	orthorhombic	{4,7}	3	(2,4)
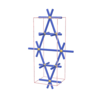
	sqc245		Cmmm	65	orthorhombic	{7,4}	3	(2,4)
	sqc250		Cmmm	65	orthorhombic	{6,6}	3	(2,4)
	sqc262		Cmmm	65	orthorhombic	{6,3}	4	(2,4)
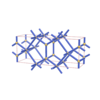
	sqc264		Cmmm	65	orthorhombic	{6,6}	3	(2,4)
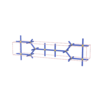
	sqc275		Cmmm	65	orthorhombic	{6,3}	4	(2,4)
	sqc278		Cmmm	65	orthorhombic	{5,4}	4	(2,5)
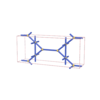
	sqc292		Cmmm	65	orthorhombic	{3,6}	4	(2,4)
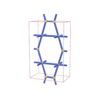
	sqc293		Cmmm	65	orthorhombic	{6,3}	4	(2,4)
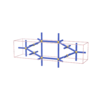
	sqc298		Cmmm	65	orthorhombic	{4,5}	4	(2,4)
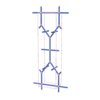
	sqc306		Cmmm	65	orthorhombic	{4,3,4}	5	(3,4)
	sqc351		Cmmm	65	orthorhombic	{10,5}	3	(2,5)
	sqc356		Cmmm	65	orthorhombic	{4,8}	3	(2,4)
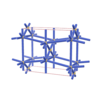
	sqc358		Cmmm	65	orthorhombic	{6,8}	3	(2,5)
	sqc390		Cmmm	65	orthorhombic	{8,4}	3	(2,5)
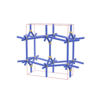
	sqc396		Cmmm	65	orthorhombic	{7,6}	3	(2,5)
	sqc397		Cmmm	65	orthorhombic	{7,3}	4	(2,5)
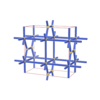
	sqc398		Cmmm	65	orthorhombic	{3,7}	4	(2,5)
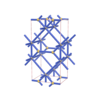
	sqc399		Cmmm	65	orthorhombic	{7,3}	4	(2,5)
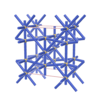
	sqc400		Cmmm	65	orthorhombic	{7,3}	4	(2,5)
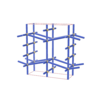
	sqc401		Cmmm	65	orthorhombic	{6,8}	3	(2,6)
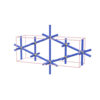
	sqc402		Cmmm	65	orthorhombic	{6,4}	4	(2,6)
	sqc407		Cmmm	65	orthorhombic	{6,8}	3	(2,5)
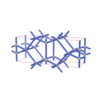
	sqc421		Cmmm	65	orthorhombic	{7,6}	3	(2,5)
	sqc429		Cmmm	65	orthorhombic	{6,4}	4	(2,5)
	sqc472		Cmmm	65	orthorhombic	{4,4,4}	5	(3,5)
	sqc497		Cmmm	65	orthorhombic	{4,4,4}	5	(3,3)
	sqc545		Cmmm	65	orthorhombic	{3,10}	5	(2,5)
	sqc549		Cmmm	65	orthorhombic	{9,4}	3	(2,5)
	sqc551		Cmmm	65	orthorhombic	{3,8}	4	(2,5)
	sqc552		Cmmm	65	orthorhombic	{8,6}	3	(2,5)
	sqc556		Cmmm	65	orthorhombic	{3,8}	4	(2,5)
	sqc561		Cmmm	65	orthorhombic	{4,7}	4	(2,6)
	sqc563		Cmmm	65	orthorhombic	{4,7}	4	(2,5)
	sqc576		Cmmm	65	orthorhombic	{4,6,4}	5	(3,4)
	sqc578		Cmmm	65	orthorhombic	{3,8}	4	(2,6)
	sqc580		Cmmm	65	orthorhombic	{8,3}	4	(2,6)
	sqc581		Cmmm	65	orthorhombic	{3,8}	4	(2,5)
	sqc589		Cmmm	65	orthorhombic	{7,4}	4	(2,6)
	sqc605		Cmmm	65	orthorhombic	{6,5}	4	(2,5)
	sqc613		Cmmm	65	orthorhombic	{6,5}	4	(2,5)
	sqc644		Cmmm	65	orthorhombic	{5,6}	4	(2,5)
	sqc650		Cmmm	65	orthorhombic	{5,6}	4	(2,5)
	sqc654		Cmmm	65	orthorhombic	{4,6}	5	(2,4)
	sqc665		Cmmm	65	orthorhombic	{4,3,4,4}	6	(4,5)
	sqc690		Cmmm	65	orthorhombic	{3,4,4}	6	(3,4)
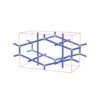
	sqc691		Cmmm	65	orthorhombic	{3,4,4}	6	(3,4)
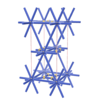
	sqc726		Cmmm	65	orthorhombic	{12,3}	5	(2,6)
	sqc735		Cmmm	65	orthorhombic	{3,9}	4	(2,6)
	sqc741		Cmmm	65	orthorhombic	{4,8}	4	(2,6)
	sqc745		Cmmm	65	orthorhombic	{9,3}	4	(2,6)
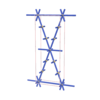
	sqc750		Cmmm	65	orthorhombic	{4,8}	5	(2,5)
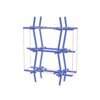
	sqc775		Cmmm	65	orthorhombic	{7,5}	4	(2,6)
	sqc799		Cmmm	65	orthorhombic	{6,6}	4	(2,6)
	sqc800		Cmmm	65	orthorhombic	{3,6}	6	(2,5)
	sqc840		Cmmm	65	orthorhombic	{3,6}	6	(2,5)
	sqc845		Cmmm	65	orthorhombic	{7,5}	4	(2,6)
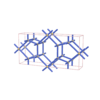
	sqc848		Cmmm	65	orthorhombic	{5,4}	5	(2,4)
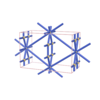
	sqc988		Cmmm	65	orthorhombic	{4,10}	5	(2,6)
	sqc996		Cmmm	65	orthorhombic	{8,5}	4	(2,6)
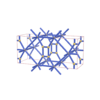
	sqc1012		Cmmm	65	orthorhombic	{7,3}	6	(2,6)
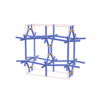
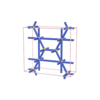
	sqc1013		Cmmm	65	orthorhombic	{3,7}	6	(2,6)
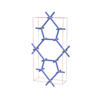
	sqc1066		Cmmm	65	orthorhombic	{8,5}	4	(2,6)
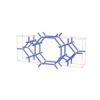
	sqc1068		Cmmm	65	orthorhombic	{5,6}	5	(2,5)
	sqc1069		Cmmm	65	orthorhombic	{5,3}	6	(2,5)
	sqc1071		Cmmm	65	orthorhombic	{5,6}	5	(2,5)
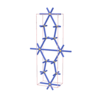
	sqc1072		Cmmm	65	orthorhombic	{3,5}	6	(2,5)
	sqc1074		Cmmm	65	orthorhombic	{5,6}	5	(2,5)
	sqc1077		Cmmm	65	orthorhombic	{4,5}	6	(2,5)
	sqc1082		Cmmm	65	orthorhombic	{3,4,4,4}	7	(4,5)
	sqc1144		Cmmm	65	orthorhombic	{8,3}	6	(2,6)
	sqc1178		Cmmm	65	orthorhombic	{8,3}	6	(2,7)
	sqc1210		Cmmm	65	orthorhombic	{6,4}	5	(2,5)
	sqc1213		Cmmm	65	orthorhombic	{4,6}	6	(2,6)
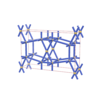
	sqc1237		Cmmm	65	orthorhombic	{6,4}	5	(2,5)
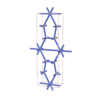
	sqc1249		Cmmm	65	orthorhombic	{5,8}	5	(2,6)
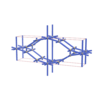
	sqc1251		Cmmm	65	orthorhombic	{5,8}	5	(2,6)
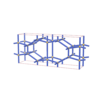
	sqc1252		Cmmm	65	orthorhombic	{4,5}	6	(2,6)
	sqc1463		Cmmm	65	orthorhombic	{3,9}	6	(2,7)
	sqc1469		Cmmm	65	orthorhombic	{4,7}	6	(2,6)
	sqc1478		Cmmm	65	orthorhombic	{4,7}	6	(2,7)