s-net search

Glossary of terms

s-net name	e.g. sqc5432
Other name
Symmetry class
Space group
Vertex transitivity
Edge transitivity
Vertices per primitive unit cell
Vertex degree(s)
Coordination sequence	any subsequence separated by spaces e.g. 4 12 30
Shortest cycle

14646 records listed.

s-net name	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
sqc6500	P4222	93	tetragonal	{4,8,4,4,8}	10	(5,6)
sqc6501	C2/c	15	monoclinic	{4,4,4,8,4}	12	(5,8)
sqc6502	Imma	74	orthorhombic	{4,4,4,8,4}	12	(5,7)
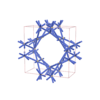
sqc6503	Imma	74	orthorhombic	{4,4,8,4,4}	12	(5,7)
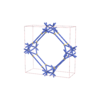
sqc6504	I4/mmm	139	tetragonal	{6,8}	8	(2,3)
sqc6505	I4/mmm	139	tetragonal	{3,8}	12	(2,3)
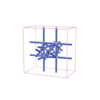
sqc6506	I4/mmm	139	tetragonal	{8,3}	12	(2,3)
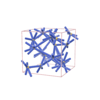
sqc6507	P4/mmm	123	tetragonal	{6,8}	8	(2,4)
sqc6508	I4122	98	tetragonal	{8,6}	8	(2,5)
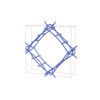
sqc6509	Cmma	67	orthorhombic	{4,6}	10	(2,6)
sqc6510	I4/mmm	139	tetragonal	{4,6}	12	(2,4)
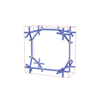
sqc6511	P42/mmc	131	tetragonal	{4,6}	12	(2,4)
sqc6512	P4/mmm	123	tetragonal	{6,4}	12	(2,4)
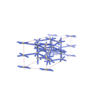
sqc6513	P4/mmm	123	tetragonal	{4,6}	12	(2,4)
sqc6514	I41/amd	141	tetragonal	{5,4}	12	(2,3)
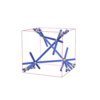
sqc6515	P4222	93	tetragonal	{4,4,8,4,8}	10	(5,6)
sqc6516	P4222	93	tetragonal	{3,8}	12	(2,7)
sqc6517	Fddd	70	orthorhombic	{8,6}	8	(2,5)
sqc6518	Fddd	70	orthorhombic	{8,6}	8	(2,5)
sqc6519	Fddd	70	orthorhombic	{3,8}	12	(2,5)
sqc6520	Fddd	70	orthorhombic	{3,8}	12	(2,5)
sqc6521	Fddd	70	orthorhombic	{3,8}	12	(2,5)
sqc6522	Cmma	67	orthorhombic	{4,8,4,4,8}	10	(5,6)
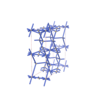
sqc6523	C2/c	15	monoclinic	{4,4,8,4,4}	12	(5,8)
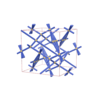
sqc6524	Imma	74	orthorhombic	{4,4,8,4,4}	12	(5,7)
sqc6525	C2/c	15	monoclinic	{4,4,8,4,4}	12	(5,8)
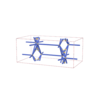
sqc6526	Imma	74	orthorhombic	{4,4,8,4,4}	12	(5,7)
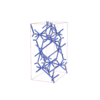
sqc6527	Cmma	67	orthorhombic	{8,3}	12	(2,7)
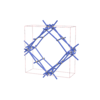
sqc6528	Fddd	70	orthorhombic	{3,8}	12	(2,5)
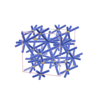
sqc6529	I4/mmm	139	tetragonal	{4,8,4}	10	(3,4)
sqc6530	I41/a	88	tetragonal	{12,6,4}	8	(3,4)
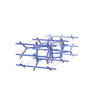
sqc6531	I41/amd	141	tetragonal	{12,6,4}	8	(3,3)
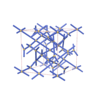
sqc6532	Imma	74	orthorhombic	{3,6,4,4,4,4}	14	(6,6)
sqc6533	C2/c	15	monoclinic	{3,6,4,4,4,4}	14	(6,7)
sqc6534	Imma	74	orthorhombic	{4,4,4,8,4}	12	(5,7)
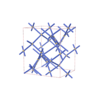
sqc6535	C2/c	15	monoclinic	{4,4,4,8,4}	12	(5,8)
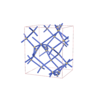
sqc6536	I212121	24	orthorhombic	{4,4,4,8,4}	12	(5,8)
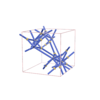
sqc6537	I4122	98	tetragonal	{8,3}	12	(2,5)
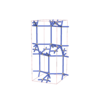
sqc6538	Cmma	67	orthorhombic	{6,4}	12	(2,7)
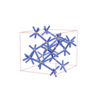
sqc6539	P4222	93	tetragonal	{6,4}	10	(2,6)
sqc6540	C2/c	15	monoclinic	{4,6,6}	10	(3,7)
sqc6541	Fddd	70	orthorhombic	{8,6}	8	(2,5)
sqc6542	Cmma	67	orthorhombic	{4,6}	10	(2,6)
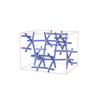
sqc6543	Fddd	70	orthorhombic	{4,6}	12	(2,5)
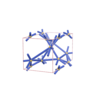
sqc6544	Cmma	67	orthorhombic	{6,4}	12	(2,7)
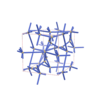
sqc6545	P4222	93	tetragonal	{6,4}	10	(2,6)
sqc6546	I4122	98	tetragonal	{4,6}	12	(2,5)
sqc6547	P42/nnm	134	tetragonal	{6,4}	10	(2,4)
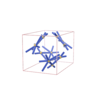
sqc6548	P-42m	111	tetragonal	{4,6}	12	(2,6)
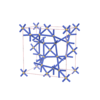
sqc6549	I-42d	122	tetragonal	{4,6}	10	(2,4)
sqc6550	Imma	74	orthorhombic	{6,4}	12	(2,7)
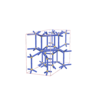
sqc6551	Imma	74	orthorhombic	{6,4}	12	(2,7)
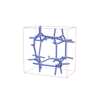
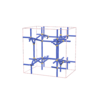
sqc6552	I-4	82	tetragonal	{6,4,4}	12	(3,7)
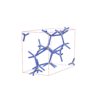
sqc6553	I-4m2	119	tetragonal	{6,4}	12	(2,6)
sqc6554	C2/c	15	monoclinic	{6,4,4}	12	(3,8)
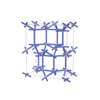
sqc6555	C2/c	15	monoclinic	{6,4,4}	12	(3,8)
sqc6556	Cmma	67	orthorhombic	{4,6}	10	(2,6)
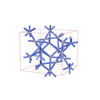
sqc6557	I4122	98	tetragonal	{4,6}	12	(2,5)
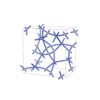
sqc6558	C2/c	15	monoclinic	{4,6,6}	10	(3,7)
sqc6559	I-42d	122	tetragonal	{6,4}	12	(2,4)
sqc6560	Fddd	70	orthorhombic	{4,6}	12	(2,5)
sqc6561	Fddd	70	orthorhombic	{4,6}	12	(2,5)
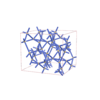
sqc6562	I4/mmm	139	tetragonal	{6,4}	12	(2,3)
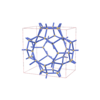
sqc6563	Fddd	70	orthorhombic	{6,4}	12	(2,5)
sqc6564	I4/mmm	139	tetragonal	{3,6,4}	14	(3,3)
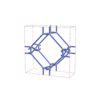
sqc6565	I-42d	122	tetragonal	{6,3,4}	14	(3,4)
sqc6566	P4/mmm	123	tetragonal	{5,4}	12	(2,4)
sqc6567	I41/a	88	tetragonal	{5,4}	12	(2,4)
sqc6568	I-42d	122	tetragonal	{5,8}	10	(2,4)
sqc6569	I-42d	122	tetragonal	{5,8}	10	(2,4)
sqc6570	P-4m2	115	tetragonal	{4,5}	12	(2,6)
sqc6571	I-4	82	tetragonal	{4,5,5}	12	(3,7)
sqc6572	P42/mmc	131	tetragonal	{5,8}	10	(2,3)
sqc6573	I4/mmm	139	tetragonal	{4,5}	12	(2,3)
sqc6574	Fddd	70	orthorhombic	{5,4}	12	(2,4)
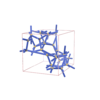
sqc6575	P42/nnm	134	tetragonal	{4,5}	12	(2,4)
sqc6576	I4122	98	tetragonal	{5,4}	12	(2,4)
sqc6577	I41/a	88	tetragonal	{5,8}	10	(2,4)
sqc6578	C2/c	15	monoclinic	{8,5,5}	10	(3,8)
sqc6579	Fddd	70	orthorhombic	{5,4}	12	(2,4)
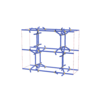
sqc6580	Cmma	67	orthorhombic	{8,5}	10	(2,7)
sqc6581	Cmma	67	orthorhombic	{4,5}	12	(2,7)
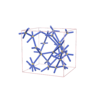
sqc6582	I-4	82	tetragonal	{4,5,5}	12	(3,7)
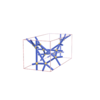
sqc6583	I212121	24	orthorhombic	{4,5,5}	12	(3,8)
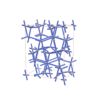
sqc6584	P4222	93	tetragonal	{5,4}	12	(2,7)
sqc6585	Fddd	70	orthorhombic	{5,4}	12	(2,4)
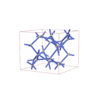
sqc6586	Fddd	70	orthorhombic	{5,4}	12	(2,4)
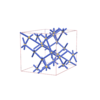
sqc6587	C2/c	15	monoclinic	{4,5,5}	12	(3,8)
sqc6588	C2/c	15	monoclinic	{4,5,5}	12	(3,8)
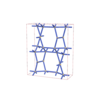
sqc6589	P-4m2	115	tetragonal	{4,5}	12	(2,6)
sqc6590	Cmma	67	orthorhombic	{4,5}	12	(2,7)
sqc6591	I41/a	88	tetragonal	{6,4}	12	(2,4)
sqc6592	I41/amd	141	tetragonal	{6,4}	12	(2,3)
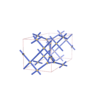
sqc6593	P42/nnm	134	tetragonal	{4,4,3}	16	(3,4)
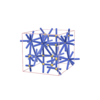
sqc6594	I41/amd	141	tetragonal	{12,4}	10	(2,3)
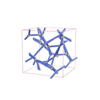
sqc6595	I4122	98	tetragonal	{4,6}	12	(2,5)
sqc6596	P4/mmm	123	tetragonal	{4,6}	12	(2,4)
sqc6597	I212121	24	orthorhombic	{4,8,4,4,4}	12	(5,8)
sqc6598	C2/c	15	monoclinic	{4,8,4,4,4}	12	(5,8)
sqc6599	C2/c	15	monoclinic	{4,4,8,4,4}	12	(5,8)