s-net search

Glossary of terms

s-net name	e.g. sqc5432
Other name
Symmetry class
Space group
Vertex transitivity
Edge transitivity
Vertices per primitive unit cell
Vertex degree(s)
Coordination sequence	any subsequence separated by spaces e.g. 4 12 30
Shortest cycle

14646 records listed.

s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
sqc200		Pmmm	47	orthorhombic	{12,6}	2	(2,5)
sqc201		Pmmm	47	orthorhombic	{12,3}	3	(2,5)
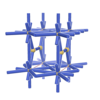
sqc202		Pmmm	47	orthorhombic	{12,3}	3	(2,5)
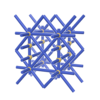
sqc203		Pmmm	47	orthorhombic	{12,3}	3	(2,5)
sqc204		Pmmm	47	orthorhombic	{10,4}	3	(2,6)
sqc205		Pmmm	47	orthorhombic	{10,4}	3	(2,6)
sqc206		Pmmm	47	orthorhombic	{8,10}	2	(2,5)
sqc207		Pmmm	47	orthorhombic	{8,10}	2	(2,5)
sqc208		Pmmm	47	orthorhombic	{4,10}	3	(2,5)
sqc209		P222	16	orthorhombic	{10,4}	3	(2,5)
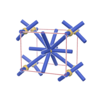
sqc210		Pmmm	47	orthorhombic	{10,4}	3	(2,5)
sqc211		P222	16	orthorhombic	{3,12}	3	(2,5)
sqc212		Cmmm	65	orthorhombic	{3,12}	3	(2,5)
sqc213		Cmmm	65	orthorhombic	{12,3}	3	(2,5)
sqc214		R-3m	166	rhombohedral	{12,6}	2	(2,2)
sqc215		Cmmm	65	orthorhombic	{10,4}	3	(2,5)
sqc216		P222	16	orthorhombic	{12,6}	2	(2,5)
sqc217		R-3m	166	rhombohedral	{12,6}	2	(2,2)
sqc218		Pmmm	47	orthorhombic	{4,10}	3	(2,6)
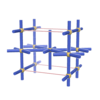
sqc219		Pmmm	47	orthorhombic	{4,6,8}	3	(3,5)
sqc220		Pmmm	47	orthorhombic	{4,6,8}	3	(3,5)
sqc221		Pmmm	47	orthorhombic	{8,4,6}	3	(3,5)
sqc222		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
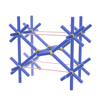
sqc223		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
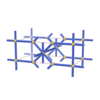
sqc224		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
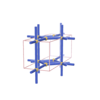
sqc225		Pmmm	47	orthorhombic	{4,3,8}	4	(3,5)
sqc226		Pmmm	47	orthorhombic	{3,8,4}	4	(3,5)
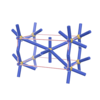
sqc227		Pmmm	47	orthorhombic	{5,8}	3	(2,5)
sqc228		P222	16	orthorhombic	{5,8}	3	(2,5)
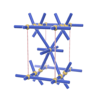
sqc229		P222	16	orthorhombic	{3,4,8}	4	(3,5)
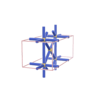
sqc230		Pmmm	47	orthorhombic	{7,4}	3	(2,4)
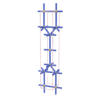
sqc231		Cmmm	65	orthorhombic	{7,4}	3	(2,5)
sqc232		Pmmm	47	orthorhombic	{6,6}	3	(2,6)
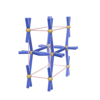
sqc233		Pmmm	47	orthorhombic	{4,7}	3	(2,4)
sqc234		P4/mmm	123	tetragonal	{8,10}	2	(2,2)
sqc235		Pmmm	47	orthorhombic	{6,8,4}	3	(3,5)
sqc236		Pmmm	47	orthorhombic	{8,6,4}	3	(3,5)
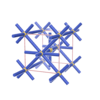
sqc237		Pmmm	47	orthorhombic	{6,8,4}	3	(3,5)
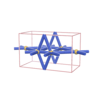
sqc238		Pmmm	47	orthorhombic	{7,4}	3	(2,4)
sqc239		Pmmm	47	orthorhombic	{4,3,8}	4	(3,5)
sqc240		Pmmm	47	orthorhombic	{3,8,4}	4	(3,5)
sqc241		Pmmm	47	orthorhombic	{4,6,8}	3	(3,4)
sqc242		Pmmm	47	orthorhombic	{4,8,6}	3	(3,5)
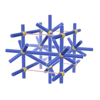
sqc243		P222	16	orthorhombic	{4,8,6}	3	(3,5)
sqc244		Cmmm	65	orthorhombic	{4,7}	3	(2,4)
sqc245		Cmmm	65	orthorhombic	{7,4}	3	(2,4)
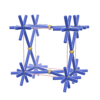
sqc246		P4/mmm	123	tetragonal	{10,4}	3	(2,2)
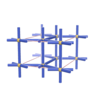
sqc247	btu	Pmmm	47	orthorhombic	{6,6}	3	(2,5)
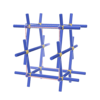
sqc248		Pmmm	47	orthorhombic	{6,6}	3	(2,5)
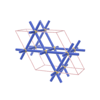
sqc249	kag	P6/mmm	191	hexagonal	{6}	3	(1,2)
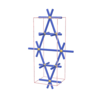
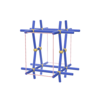
sqc250		Cmmm	65	orthorhombic	{6,6}	3	(2,4)
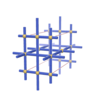
sqc251		Pmmm	47	orthorhombic	{6,3}	4	(2,5)
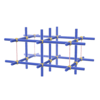
sqc252		Pmmm	47	orthorhombic	{4,4,4,6}	4	(4,6)
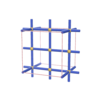
sqc253		Pmmm	47	orthorhombic	{4,4,6,4}	4	(4,6)
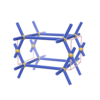
sqc254		P4/mmm	123	tetragonal	{4,6,4}	4	(3,3)
sqc255		Pmmm	47	orthorhombic	{7,4}	3	(2,4)
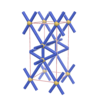
sqc256		P222	16	orthorhombic	{4,7}	3	(2,4)
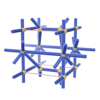
sqc257		Pmmm	47	orthorhombic	{4,7}	3	(2,4)
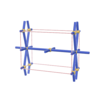
sqc258		P222	16	orthorhombic	{4,8,3}	4	(3,5)
sqc259		Pmmm	47	orthorhombic	{3,8,4}	4	(3,5)
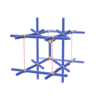
sqc260		Pmmm	47	orthorhombic	{3,4,8}	4	(3,5)
sqc261		P222	16	orthorhombic	{4,3,8}	4	(3,5)
sqc262		Cmmm	65	orthorhombic	{6,3}	4	(2,4)
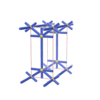
sqc263		Pmmm	47	orthorhombic	{6,6}	3	(2,5)
sqc264		Cmmm	65	orthorhombic	{6,6}	3	(2,4)
sqc265		Pmmm	47	orthorhombic	{6,6}	3	(2,5)
sqc266		Pmmm	47	orthorhombic	{6,6}	3	(2,5)
sqc267		Pmmm	47	orthorhombic	{4,6,4}	4	(3,5)
sqc268		Pmmm	47	orthorhombic	{4,4,6}	4	(3,5)
sqc269		Pmmm	47	orthorhombic	{4,4,6}	4	(3,5)
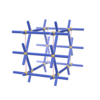
sqc270		Pmmm	47	orthorhombic	{4,4,6}	4	(3,5)
sqc271		Pmmm	47	orthorhombic	{4,6,4}	4	(3,5)
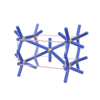
sqc272		P222	16	orthorhombic	{6,6}	3	(2,5)
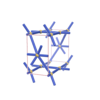
sqc273		P222	16	orthorhombic	{4,6,4}	4	(3,5)
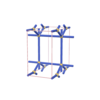
sqc274		Pmmm	47	orthorhombic	{6,3}	4	(2,5)
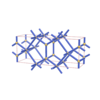
sqc275		Cmmm	65	orthorhombic	{6,3}	4	(2,4)
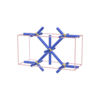
sqc276		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
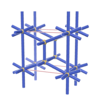
sqc277		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
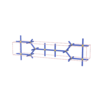
sqc278		Cmmm	65	orthorhombic	{5,4}	4	(2,5)
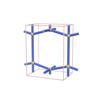
sqc279		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
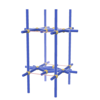
sqc280		Pmmm	47	orthorhombic	{4,5}	4	(2,5)
sqc281		Pmmm	47	orthorhombic	{4,8,3}	4	(3,5)
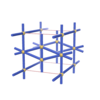
sqc282		Pmmm	47	orthorhombic	{4,4,6}	4	(3,5)
sqc283		Pmmm	47	orthorhombic	{6,4,4,4}	4	(4,4)
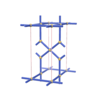
sqc284	yav-d	P6/mmm	191	hexagonal	{4,6}	4	(2,2)
sqc285		Pmmm	47	orthorhombic	{4,4,3,4}	5	(4,4)
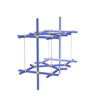
sqc286		Pmmm	47	orthorhombic	{4,3,4,4}	5	(4,4)
sqc287		Pmmm	47	orthorhombic	{3,4,4,4}	5	(4,4)
sqc288		P222	16	orthorhombic	{6,6}	3	(2,5)
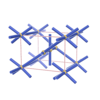
sqc289		P222	16	orthorhombic	{6,6}	3	(2,5)
sqc290		P222	16	orthorhombic	{6,4,4}	4	(3,5)
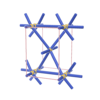
sqc291		P222	16	orthorhombic	{4,6,4}	4	(3,5)
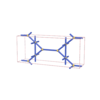
sqc292		Cmmm	65	orthorhombic	{3,6}	4	(2,4)
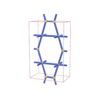
sqc293		Cmmm	65	orthorhombic	{6,3}	4	(2,4)
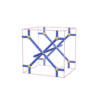
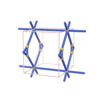
sqc294		P4/mmm	123	tetragonal	{3,6}	5	(2,3)
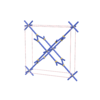
sqc295		Pmmm	47	orthorhombic	{3,6}	5	(2,4)
sqc296		I4/mmm	139	tetragonal	{3,6}	5	(2,3)
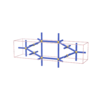
sqc297		Pmmm	47	orthorhombic	{5,4}	4	(2,5)
sqc298		Cmmm	65	orthorhombic	{4,5}	4	(2,4)
sqc299		P222	16	orthorhombic	{4,4,3}	5	(3,5)