h-net: hqc113

Topological data

Orbifold symbol	*2224
Transitivity (vertex, edge, ring)	(2,3,2)
Vertex degrees	{8,4}
2D vertex symbol	{4.3.3.4.4.3.3.4}{3.3.3.3}
Vertex coordination sequence	[(8, 32, 120, 448, 1672, 6240, 23288, 86912), (4, 20, 80, 300, 1112, 4164, 15520, 57948)]
Delaney-Dress Symbol	<113.2:5:1 2 3 5,2 4 5,1 3 4 5:4 3,8 4>
Dual net	hqc138

Derived s-nets

s-nets with faithful topology

23 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
	sqc391		P4/mmm	123	tetragonal	{8,4}	3	(2,3)
	sqc3361		I4/mmm	139	tetragonal	{4,8}	6	(2,3)
	sqc3378		I4/mmm	139	tetragonal	{8,4}	6	(2,4)
	sqc3516		Fmmm	69	orthorhombic	{8,8,4}	6	(3,5)
	sqc9369		I4122	98	tetragonal	{8,4}	12	(2,6)
	sqc9377		I4122	98	tetragonal	{8,8,4}	12	(3,6)
	sqc9432		I41/acd	142	tetragonal	{8,4}	12	(2,3)
	sqc9447		I4122	98	tetragonal	{8,4}	12	(2,6)
	sqc9468		Fddd	70	orthorhombic	{8,4}	12	(2,6)
	sqc9475		I4122	98	tetragonal	{8,8,4}	12	(3,6)
	sqc9503		Fddd	70	orthorhombic	{8,4}	12	(2,6)
	sqc9504		Fddd	70	orthorhombic	{8,8,4}	12	(3,6)
	sqc9505		Fddd	70	orthorhombic	{8,8,4}	12	(3,6)
	sqc9657		I41/acd	142	tetragonal	{8,4}	12	(2,3)
	sqc479		I4/mmm	139	tetragonal	{4,8}	3	(2,3)
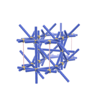
	sqc3168		P4222	93	tetragonal	{4,8,8}	6	(3,5)
	sqc3171		Cmma	67	orthorhombic	{8,4,8}	6	(3,5)
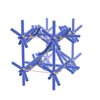
	sqc3172		P4222	93	tetragonal	{4,8,8}	6	(3,5)
	sqc3201		P4222	93	tetragonal	{8,4}	6	(2,5)
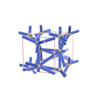
	sqc3394		P4222	93	tetragonal	{4,8}	6	(2,5)
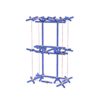
	sqc3447		Cmma	67	orthorhombic	{8,4}	6	(2,5)
	sqc3551		Cmma	67	orthorhombic	{8,4}	6	(2,5)
	sqc3750		P42/nnm	134	tetragonal	{8,4}	6	(2,3)

s-nets with edge collapse

show / hide

Derived U-tilings

10 records listed.

Image	U-tiling name	PGD Subgroup	Transitivity (Vert,Edge,Face)	Vertex Degree	Vertex Symbol	P net	G net	D net
	UQC111	*2224	(2,3,2)	{8,4}	{4.3.3.4.4.3.3.4}{3.3.3.3}	sqc391	sqc9432	sqc3750
	UQC112	*2224	(2,3,2)	{8,4}	{4.3.3.4.4.3.3.4}{3.3.3.3}	sqc3361	sqc9657	sqc479
	UQC1821	*22222a	(2,5,4)	{8,4}	{4.3.3.4.4.3.3.4}{3.3.3.3}	sqc8420	sqc9369	sqc3201
	UQC1822	*22222b	(2,5,4)	{8,4}	{4.3.3.4.4.3.3.4}{3.3.3.3}	sqc2622	sqc9503	sqc3447
	UQC1823	*22222a	(2,5,4)	{8,4}	{4.3.3.4.4.3.3.4}{3.3.3.3}	sqc8866	sqc9447	sqc3394
	UQC1824	*22222b	(2,5,4)	{8,4}	{4.3.3.4.4.3.3.4}{3.3.3.3}	sqc3378	sqc9468	sqc3551
	UQC4152	*22222a	(3,5,2)	{8,8,4}	{4.3.3.4.4.3.3.4}{4.4.3.3.4.4.3....	sqc9272	sqc9377	sqc3168
	UQC4153	*22222b	(3,5,2)	{8,8,4}	{4.3.3.4.4.3.3.4}{4.4.3.3.4.4.3....	sqc3070	sqc9505	sqc3171
	UQC4154	*22222b	(3,5,2)	{8,8,4}	{4.3.3.4.4.3.3.4}{4.4.3.3.4.4.3....	sqc3516	sqc9504	sqc391
	UQC4155	*22222a	(3,5,2)	{8,8,4}	{4.3.3.4.4.3.3.4}{4.4.3.3.4.4.3....	sqc9277	sqc9475	sqc3172

Symmetry-lowered hyperbolic tilings

show / hide