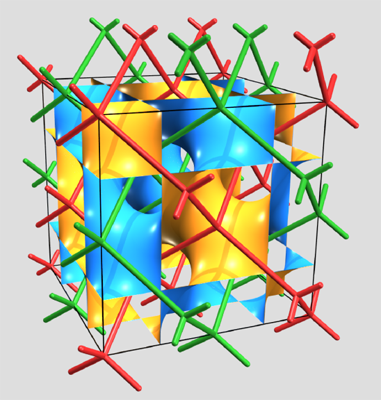
The Diamond (D) surface

The discovery of the D surface is —like the P — due to Schwarz, with input from his teachers Weierstrass and Riemann (see Nitsche ). Schwarz realised that a Flächenstuck bounded by a tetrahedral Petrie polygon could be globally extended in 3D euclidean space via rotations to form an infinite crystalline surface without self-intersection; thus the D surface was the first explicitly known TPMS.

(image courtesy of Gerd Schröder-Turk)

The non-oriented / oriented surface has space group symmetries Pn-3m / Fd-3m. The face-centred cell of the oriented space group is why the D surface is also called the F surface. The name diamond surface comes from its labyrinth graphs: these are a pair of interwoven networks each with the bonding structure of diamond ( dia in the notation of O'Keeffe). This pattern can also be formed by a decoration on the D surface.

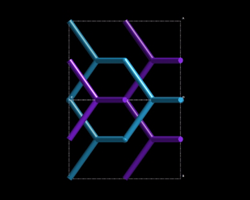
View down [100]	View down [111]	View down [110]

While the P surface bisects the platonic octahedron, the D surface bisects the platonic tetrahedron as the minimal surface spanning the Petrie polygon of the tetrahedron. It shares identical 2D intrinsic geometry with the P and G surfaces, all have hyperbolic surface orbifold of *246. In contrast to its Bonnet adjoint surface (the P), a smallest Flächenstuck for the D is bounded by euclidean symmetry operations consisting of a pair of in-surface two-fold rotations about straight lines meeting at π/2, and a single mirror plane. Like the P, the D surface has lower symmetry variants, including tetragonal and orthorhombic examples.

Return to the EPINET mathematical background page.