The Mathematics behind the EPINET Project

The EPINET project contributes to the enumeration of periodic networks in three–dimensional euclidean space (E³). These networks are of interest to geometers, structural chemists, and statistical physicists.

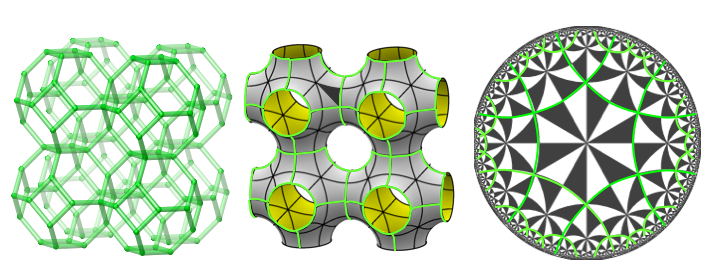
The following images show the framework structure of sodalite, which can be embedded on the P surface as shown in the middle. The network forms a tiling of the P surface which unwraps in the hyperbolic plane to a tiling by hexagons.

This project draws on several areas of geometry and crystallography. The following pages give illustrated and non-technical explanations of the key concepts.

Mathematical background

• A gentle introduction to hyperbolic geometry and the Poincaré disc model from The Institute for Figuring.
• Minimal surfaces, in general, and those used within EPINET: the primitive, P, diamond, D, and gyroid, G, periodic minimal surfaces.
• The covering maps that wrap the hyperbolic plane onto a triply periodic minimal surface.
• How to enumerate tilings of the hyperbolic plane that are compatible with the covering maps. We use Conway's orbifold notation for 2D discrete symmetry groups, and algorithms from combinatorial tiling theory.
• The surface reticulations that result from projecting the hyperbolic tilings onto each periodic minimal surface and the corresponding aspects of network topology.
• The technical terms used across this site are explained in the site glossary.

Related Work

• A brief summary of other approaches to enumerating 3-periodic networks, and a note on the history of the EPINET project.
• Papers, suggested further reading and links to related websites are collected on the site bibliography.