The Gyroid

The G surface or gyroid is a relative newcomer to the stable: it was discovered experimentally by Alan Schoen in the 1960's. It is a remarkable structure, mathematically subtle and not readily amenable to the parametrisations used by Schwarz et. al. to derive the simpler P and D examples. It is (so far) the most ubiquitous TPMS found in physical systems, most likely due to its combination of local homogeneity (like the P and D surfaces) and global homogeneity. (This can be defined in a number of ways; we prefer a technique developed by Gerd Schröder, based on rigorous definitions of the labyrinthine skeleta; see G.E. Schroeder, S.J. Ramsden, A.G. Christy and S.T. Hyde, “Medial Surfaces of Hyperbolic Structures”, Eur. Phys. J. B, 35:551-564, (2003).)

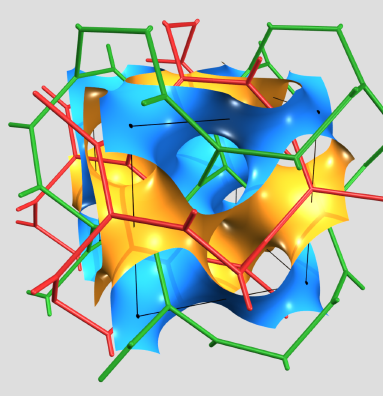(image courtesy of Gerd Schröder-Turk)

Like the P and D surfaces, the gyroid has 2D intrinsic symmetry related to the hyperbolic group *246. However, none of the hyperbolic mirror lines map to 3D euclidean symmetries, so that it is entirely free of straight lines and mirror planes. Its non-oriented / oriented space group pair is Ia-3d / I4(1)32. The latter space group is chiral and implies that a single subvolume of the bicontinuous structure is chiral. As it lacks straight lines, the gyroid is not balanced . However, the pair of subvolumes are related to each other by a 3D inversion symmetry (through any flat point on the surface). So while one labyrinth of the spatial partition induced by the gyroid is right-handed and the other is left-handed, the G surface itself is not chiral. The labyrinth graph contains a pair of nets, each known to crystallographers as Wells' (10,3)-a net, the chiral 3-coordinated network with vertices on sites of the Y* lattice complex (+Y* or -Y* depending on the handedness). The edges of the labyrinth graph represent channels and they meet in triples at planar 2π/3 junctions. The (10,3)-a network is also O'Keeffe's srs structure.

	View down [100]	View down [111]	View down [110]

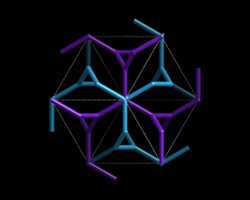
The absence of mirrors and in-surface straight lines means that the symmetry operations of the hyperbolic orbifold (*246) are not manifest as 3D Euclidean isometries. Rather, the pure rotational orbifold 246 (an order-2 subgroup of *246) denotes the hyperbolic group corresponding to Ia-3d. This situation means a 2D hyperbolic chiral pattern will map to a pair of distinct reticulations of the Gyroid (unlike the P or D where hyperbolic tilings define a unique reticulation of the surface). See our paper "A note on the two symmetry-preserving covering maps of the Gyroid minimal surface" [DOI link] for more details.

Return to the EPINET mathematical background page.