h-net: hqc2002
Topological data
| Orbifold symbol | *22222 |
| Transitivity (vertex, edge, ring) | (2,6,4) |
| Vertex degrees | {3,6} |
| 2D vertex symbol | {4.4.8}{8.4.4.8.4.4} |
| Delaney-Dress Symbol | <2002.2:12:1 2 3 5 7 8 9 10 11 12,2 4 10 8 9 12,3 8 6 7 9 11 12:4 8 4 4,3 6> |
| Dual net | hqc2037 |
Derived s-nets
s-nets with faithful topology
23 records listed.| Image | s-net name | Other names | Space group | Space group number | Symmetry class | Vertex degree(s) | Vertices per primitive unit cell | Transitivity (Vertex, Edge) |
|---|---|---|---|---|---|---|---|---|
|
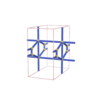
sqc801 | Pmmm | 47 | orthorhombic | {3,6} | 6 | (2,6) | |
|
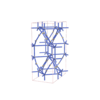
sqc5047 | Fmmm | 69 | orthorhombic | {3,6} | 12 | (2,6) | |
|
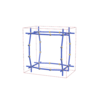
sqc10912 | P4/mmm | 123 | tetragonal | {6,3} | 24 | (2,6) | |
|
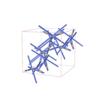
sqc10707 | I4122 | 98 | tetragonal | {6,3,3} | 24 | (3,7) | |
|
sqc10759 | I4122 | 98 | tetragonal | {6,3,3} | 24 | (3,7) | |
|
sqc10800 | Fddd | 70 | orthorhombic | {6,3,3} | 24 | (3,7) | |
|
sqc10804 | I4122 | 98 | tetragonal | {6,3,3} | 24 | (3,7) | |
|
sqc10807 | Fddd | 70 | orthorhombic | {6,3,3} | 24 | (3,7) | |
|
sqc10813 | Fddd | 70 | orthorhombic | {6,3,3} | 24 | (3,7) | |
|
sqc10816 | Fddd | 70 | orthorhombic | {6,3,3} | 24 | (3,7) | |
|
sqc10817 | Fddd | 70 | orthorhombic | {6,3,3} | 24 | (3,7) | |
|
sqc10882 | I4122 | 98 | tetragonal | {6,3,3} | 24 | (3,7) | |
|
sqc11045 | I4122 | 98 | tetragonal | {6,3,3} | 24 | (3,7) | |
|
sqc803 | Pmmm | 47 | orthorhombic | {3,6} | 6 | (2,6) | |
|
sqc901 | Pmmm | 47 | orthorhombic | {3,6} | 6 | (2,6) | |
|
sqc4875 | P4222 | 93 | tetragonal | {3,6} | 12 | (2,6) | |
|
sqc5039 | P4222 | 93 | tetragonal | {3,6} | 12 | (2,6) | |
|
sqc5048 | Cmma | 67 | orthorhombic | {6,3} | 12 | (2,6) | |
|
sqc5073 | P4222 | 93 | tetragonal | {3,6} | 12 | (2,6) | |
|
sqc5314 | Cmma | 67 | orthorhombic | {3,6} | 12 | (2,6) | |
|
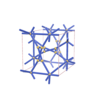
sqc5364 | P4222 | 93 | tetragonal | {3,6} | 12 | (2,6) | |
|
sqc5366 | P4222 | 93 | tetragonal | {3,6} | 12 | (2,6) |
s-nets with edge collapse
Derived U-tilings
10 records listed.| Image | U-tiling name | PGD Subgroup | Transitivity (Vert,Edge,Face) | Vertex Degree | Vertex Symbol | P net | G net | D net |
|---|---|---|---|---|---|---|---|---|
 |
UQC2344 | *22222a | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} | No s‑net |
sqc10707
|
sqc4875
|
 |
UQC2345 | *22222a | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} |
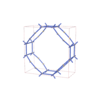sqc10429
|
sqc10759
|
sqc5039
|
 |
UQC2346 | *22222b | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} |
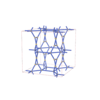sqc4622
|
sqc10816
|
sqc901
|
 |
UQC2347 | *22222b | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} |
sqc801
|
sqc10800
|
sqc5314
|
 |
UQC2348 | *22222b | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} | No s‑net |
sqc10817
|
sqc803
|
 |
UQC2349 | *22222b | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} |
sqc5047
|
sqc10807
|
sqc801
|
 |
UQC2350 | *22222b | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} |
sqc801
|
sqc10813
|
sqc5048
|
 |
UQC2351 | *22222a | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} | No s‑net |
sqc11045
|
sqc5366
|
 |
UQC2352 | *22222a | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} |
sqc10912
|
sqc10882
|
sqc5364
|
 |
UQC2353 | *22222a | (2,6,4) | {6,3} | {4.4.8}{8.4.4.8.4.4} |
sqc4619
|
sqc10804
|
sqc5073
|
