Triply Periodic Minimal surfaces

Minimal surfaces

Minimal surfaces are defined within the language of differential geometry as surfaces of zero mean curvature. This means they are equally convex and concave at all points and their form is therefore saddle–like, or hyperbolic .

They are called minimal because given a fixed boundary curve the area of a “minimal surface” is extremal with respect to other surfaces with the same boundary. A soap film minimizes its area under surface tension, so dipping a wire frame into soapy water produces a minimal surface geometry, as the following example illustrates.

Minimal surface soap film

The simplest examples of minimal surfaces are the catenoid and helicoid which are illustrated below. (Images are courtesy of Matthias Weber ). The second illustration below is a one–periodic surface: it has a 1D lattice of translations.

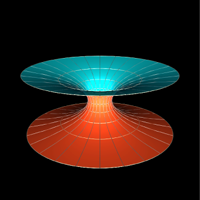
Catenoid minimal surface	Helicoid minimal surface

Periodic minimal surfaces

Three–periodic minimal surfaces have three lattice vectors, i.e., they are invariant under translation along three independent directions. They are also called triply–periodic or infinite periodic minimal surfaces, abbreviated to TPMS and IPMS , respectively. Numerous examples are now known with cubic, tetragonal, rhombohedral, and orthorhombic symmetries. Monoclinic and triclinic examples are certain to exist, though difficult to parametrise. An interesting open question is the existence of “glassy” infinite genus minimal surfaces without any exact translational symmetry.

See the bibliography for links to some image galleries.

The symmetries of a TPMS allow the surface to be constructed from a single asymmetric surface patch (also called a Flächenstuck ), which extends to the entire surface under the action of the symmetry group. The most important local symmetries of minimal surfaces are euclidean reflections (in mirror planes) and two–fold rotations. Simple examples of these symmetries (in a non-periodic minimal surface) can be seen here.

These symmetries are readily detected from the geometry of a minimal surface. Mirror planes result in plane lines of curvature on the surface (with the jargon of differential geometry this means the principal directions on the surface lie in a plane). Two–fold rotation axes lying in the surface are necessarily straight lines (linear asymptotes). These symmetries, and special properties of the Gauss map of minimal surfaces can be used to parametrise and exhaustively enumerate the simpler “regular” TPMS.

Surfaces Used Within Epinet

The P, D, and G Surfaces

The primitive (P) , diamond (D) and gyroid (G) surfaces are identical in a 2D non–euclidean sense. That is why we can generate tilings on all of them from a single 2D hyperbolic ( H² ) tiling. They do have, however, very different global embeddings in 3D Euclidean ( E³ ) space. Those differences are due to distinct ways of projecting H² structure into E³ . This process is similar to, but more complex than, the multiple ways that a Euclidean planar hexagonal pattern can be wrapped onto a cylinder to give carbon nanotube (buckytube) structures.

The following three illustrations show primitive translational unit cells for the three surfaces derived from the same dodecagonal patch of the hyperbolic plane.

P surface	D surface	G surface

These three cubic surfaces have assumed increasing importance in understanding structures of atomic, molecular and macromolecular systems, as they define partitions of space found in crystals and liquid crystals. You can find a more detailed exploration in the book “The Language of Shape” (Elsevier, 1997). Their occurrence in physical systems is likely due to their very low inhomogeneity of Gaussian curvature—they are (in some loose sense that remains not well defined!) the least perturbed embeddings of the hyperbolic plane in 3D Euclidean ( E³ ) space.

The properties of these surfaces are described in detail on separate EPINET background pages: primitive (P) surface , diamond (D) surface and gyroid (G) surface .

Labyrinth Spaces and TPMS

Like any infinite surface, a TPMS carves 3D space into a pair of sub–volumes. Since two–fold axes exchange sides of the surface, TPMS containing straight lines cleave space into two identical sub–volumes. We call such examples of TPMS minimal balance surfaces . Koch and Fischer derived many examples of such TPMS by analysing the surfaces spanning all the 2–fold axis line arrays permitted by the 230 3D space groups.

The shape of a TPMS is often described by the geometry of the pair of sub–volumes. These, in turn, are often described by a labyrinth graph —a network whose edges describe the channels of the sub–volume. This concept has been put on a more rigorous basis for TPMS by Gerd Schröder (see G.E. Schroeder, S.J. Ramsden, A.G. Christy and S.T. Hyde, “Medial Surfaces of Hyperbolic Structures”, Eur. Phys. J. B, 35:551–564, (2003).) From this perspective, we can understand a TPMS loosely as the Voronoi walls between pairs of interwoven 3D networks.

The following image (courtesy of Gerd Schröder) shows the labyrinth graphs of the P surface .

P surface labyrinth

Polycontinuous Triply Periodic Minimal Complexes

The notion of minimal surfaces carving up space in a bicontinuous way can be generalised to find (possibly branched) triply periodic minimal surfaces that cleave 3D space into more than two sub–volumes. These are polycontinuous TPMS .

The following image is of a branched chiral cubic surface which carves space into three equivalent volumes (our analysis of this surface is not yet published).

A polycontinuous partition of space.

Unfortunately, the term “polycontinuous” has been used in many senses. The simplest way to cleave space into more than two sub–volumes is to form a series of parallel surface laminations of TPMS. That leaves the two labyrinth sub–volumes and constant thickness sheaves following the TPMS topology. See, for example, R Holyst “Liquid crystals: Infinite networks of surfaces”, Nature Materials 4:510–511 (2005). [ DOI link ].

Return to the EPINET mathematical background page.