s-net search

Glossary of terms

s-net name	e.g. sqc5432
Other name
Symmetry class
Space group
Vertex transitivity
Edge transitivity
Vertices per primitive unit cell
Vertex degree(s)
Coordination sequence	any subsequence separated by spaces e.g. 4 12 30
Shortest cycle

14646 records listed.

s-net name	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
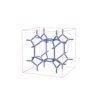
sqc12000	I41/acd	142	tetragonal	{4,4,4}	28	(3,4)
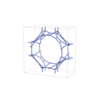
sqc12001	P42/mmc	131	tetragonal	{3,4}	32	(2,6)
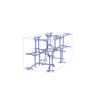
sqc12002	I4/mmm	139	tetragonal	{4,3}	32	(2,6)
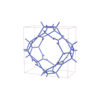
sqc12003	I41/amd	141	tetragonal	{3,4}	32	(2,6)
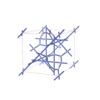
sqc12004	P4/mmm	123	tetragonal	{3,3,4,4,4,4}	32	(6,6)
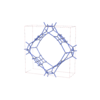
sqc12005	P42/nnm	134	tetragonal	{3,4,4,4,4,4}	30	(6,6)
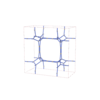
sqc12006	I4/mmm	139	tetragonal	{3,4,4,4,4,4}	30	(6,6)
sqc12007	I4/mmm	139	tetragonal	{3,4}	32	(2,6)
sqc12008	I41/acd	142	tetragonal	{4,4,4}	28	(3,4)
sqc12009	Fddd	70	orthorhombic	{3,3,4,4}	32	(4,7)
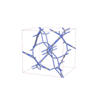
sqc12010	Fddd	70	orthorhombic	{3,3,4,4}	32	(4,7)
sqc12011	I41/a	88	tetragonal	{3,3,4,4}	32	(4,7)
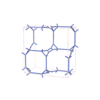
sqc12012	P4/nmm	129	tetragonal	{3,4}	32	(2,6)
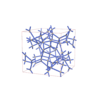
sqc12013	I41/acd	142	tetragonal	{4,4,4}	28	(3,4)
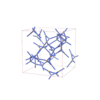
sqc12014	I4122	98	tetragonal	{3,3,4,4}	32	(4,7)
sqc12015	P4/mmm	123	tetragonal	{3,4}	32	(2,6)
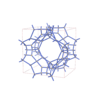
sqc12016	I4/mmm	139	tetragonal	{4,4,4,3,4,4}	30	(6,6)
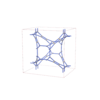
sqc12017	P42/nnm	134	tetragonal	{4,4,3,4,4,4}	30	(6,6)
sqc12018	I4/mmm	139	tetragonal	{4,3}	32	(2,6)
sqc12019	I4/mmm	139	tetragonal	{4,3}	32	(2,6)
sqc12020	P42/mmc	131	tetragonal	{3,4}	32	(2,6)
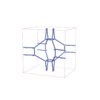
sqc12021	I-42d	122	tetragonal	{3,3,4,4}	32	(4,7)
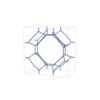
sqc12022	P42/mmc	131	tetragonal	{3,4}	32	(2,6)
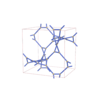
sqc12023	I4/mmm	139	tetragonal	{3,4}	32	(2,6)
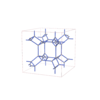
sqc12024	P42/nnm	134	tetragonal	{4,3}	32	(2,6)
sqc12025	I4/mmm	139	tetragonal	{3,4}	32	(2,6)
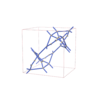
sqc12026	I41/a	88	tetragonal	{3,3,4,4}	32	(4,7)
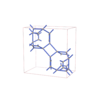
sqc12027	P42/nnm	134	tetragonal	{3,4}	32	(2,6)
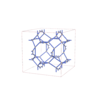
sqc12028	P4/nmm	129	tetragonal	{3,4}	32	(2,6)
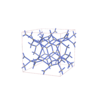
sqc12029	I4/mmm	139	tetragonal	{3,4}	32	(2,6)
sqc12030	I41/acd	142	tetragonal	{3,4}	32	(2,4)
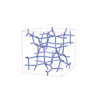
sqc12031	I41/acd	142	tetragonal	{3,4}	32	(2,4)
sqc12032	I41/acd	142	tetragonal	{3,4}	32	(2,4)
sqc12033	I41/acd	142	tetragonal	{3,4}	32	(2,5)
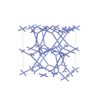
sqc12034	I41/acd	142	tetragonal	{3,4}	32	(2,5)
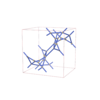
sqc12035	I41/acd	142	tetragonal	{4,3,4}	32	(3,4)
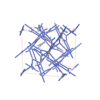
sqc12036	P42/nnm	134	tetragonal	{4,3}	32	(2,6)
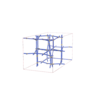
sqc12037	I41/acd	142	tetragonal	{4,3,4}	32	(3,4)
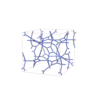
sqc12038	I41/amd	141	tetragonal	{3,4}	32	(2,6)
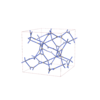
sqc12039	I41/acd	142	tetragonal	{3,3,4}	36	(3,4)
sqc12040	I41/acd	142	tetragonal	{3,3,4}	36	(3,4)
sqc12041	I41/acd	142	tetragonal	{3,3,4}	36	(3,4)
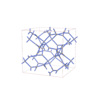
sqc12042	I41/acd	142	tetragonal	{3,3,4}	36	(3,4)
sqc12043	P4/mmm	123	tetragonal	{3,4,3,4,4,4}	32	(6,7)
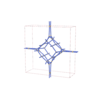
sqc12044	P4/mmm	123	tetragonal	{3,4,3,4,4,4}	32	(6,7)
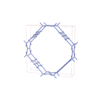
sqc12045	P4/mmm	123	tetragonal	{3,4,4,3,4,4}	32	(6,7)
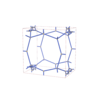
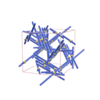
sqc12046	P4/mmm	123	tetragonal	{3,4,4,3,4,4}	32	(6,7)
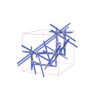
sqc12047	I4122	98	tetragonal	{7,4,4}	24	(3,8)
sqc12048	I4122	98	tetragonal	{7,4,4}	24	(3,8)
sqc12049	I4122	98	tetragonal	{5,5,5}	24	(3,8)
sqc12050	F-43m	216	cubic	{4,12}	18	(2,4)
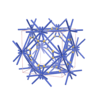
sqc12051	P-43m	215	cubic	{3,16}	27	(2,4)
sqc12052	Pm-3m	221	cubic	{3,16}	27	(2,4)
sqc12053	Im-3m	229	cubic	{12,3}	28	(2,3)
sqc12054	Fd-3m	227	cubic	{12,3}	28	(2,3)
sqc12055	Ia-3	206	cubic	{12,3}	28	(2,3)
sqc12056	I4122	98	tetragonal	{7,4,4}	24	(3,8)
sqc12057	I213	199	cubic	{4,12}	18	(2,5)
sqc12058	Fddd	70	orthorhombic	{7,4,4}	24	(3,8)
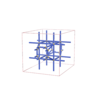
sqc12059	I4122	98	tetragonal	{7,4,4}	24	(3,8)
sqc12060	P4/mmm	123	tetragonal	{7,4}	24	(2,7)
sqc12061	P4232	208	cubic	{4,12}	18	(2,4)
sqc12062	Fddd	70	orthorhombic	{7,4,4}	24	(3,8)
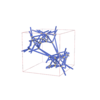
sqc12063	Fddd	70	orthorhombic	{7,4,4}	24	(3,8)
sqc12064	I4122	98	tetragonal	{7,4,4}	24	(3,8)
sqc12065	I4122	98	tetragonal	{3,6,6}	24	(3,8)
sqc12066	I4122	98	tetragonal	{3,6,6}	24	(3,8)
sqc12067	I4122	98	tetragonal	{3,6,6}	24	(3,8)
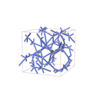
sqc12068	I4122	98	tetragonal	{3,6,6}	24	(3,8)
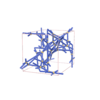
sqc12069	I4122	98	tetragonal	{3,6,6}	24	(3,8)
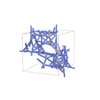
sqc12070	I4122	98	tetragonal	{5,5,5}	24	(3,8)
sqc12071	I4122	98	tetragonal	{5,5,5}	24	(3,8)
sqc12072	Fddd	70	orthorhombic	{5,5,5}	24	(3,8)
sqc12073	Fddd	70	orthorhombic	{5,5,5}	24	(3,8)
sqc12074	Fddd	70	orthorhombic	{5,5,5}	24	(3,8)
sqc12075	Fddd	70	orthorhombic	{5,5,5}	24	(3,8)
sqc12076	I4122	98	tetragonal	{4,4,4,3,4,4}	32	(6,8)
sqc12077	Fddd	70	orthorhombic	{4,4,4,3,4,4}	32	(6,8)
sqc12078	I4122	98	tetragonal	{4,4,4,3,4,4}	32	(6,8)
sqc12079	Fddd	70	orthorhombic	{4,4,4,3,4,4}	32	(6,8)
sqc12080	Fddd	70	orthorhombic	{4,4,4,3,4,4}	32	(6,8)
sqc12081	Fddd	70	orthorhombic	{4,4,3,4,4,4}	32	(6,8)
sqc12082	Fddd	70	orthorhombic	{4,4,3,4,4,4}	32	(6,8)
sqc12083	I4122	98	tetragonal	{4,4,3,4,4,4}	32	(6,8)
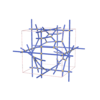
sqc12084	I4122	98	tetragonal	{4,4,3,4,4,4}	32	(6,8)
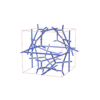
sqc12085	P4232	208	cubic	{3,4,3,4}	34	(4,5)
sqc12086	P4232	208	cubic	{4,4,3,3}	34	(4,5)
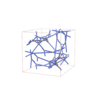
sqc12087	Fddd	70	orthorhombic	{4,4,3,4,4,4}	32	(6,8)
sqc12088	I4122	98	tetragonal	{4,4,4,3,4,4}	32	(6,8)
sqc12089	I4122	98	tetragonal	{4,3,4,4,4,4}	32	(6,8)
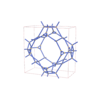
sqc12090	P4232	208	cubic	{4,3,3,4}	34	(4,5)
sqc12091	P4/mmm	123	tetragonal	{4,3,4,4,4,4}	32	(6,7)
sqc12092	I4122	98	tetragonal	{4,3,4,4,4,4}	32	(6,8)
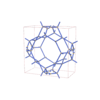
sqc12093	P4/mmm	123	tetragonal	{4,3,4,4,4,4}	32	(6,7)
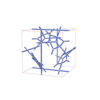
sqc12094	P4232	208	cubic	{3,4,3,4}	34	(4,5)
sqc12095	I4122	98	tetragonal	{4,3,4,4,4,4}	32	(6,8)
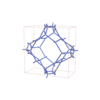
sqc12096	P4/mmm	123	tetragonal	{4,3,4,4,4,4}	32	(6,7)
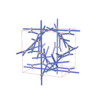
sqc12097	P4232	208	cubic	{3,3,6,4}	34	(4,5)
sqc12098	P4232	208	cubic	{4,3,3,4}	34	(4,5)
sqc12099	P4232	208	cubic	{3,4,4,3}	34	(4,5)