s-net search

Glossary of terms

s-net name	e.g. sqc5432
Other name
Symmetry class
Space group
Vertex transitivity
Edge transitivity
Vertices per primitive unit cell
Vertex degree(s)
Coordination sequence	any subsequence separated by spaces e.g. 4 12 30
Shortest cycle

14646 records listed.

s-net name	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
sqc12900	P4232	208	cubic	{7,3}	36	(2,6)
sqc12901	P4232	208	cubic	{7,3}	36	(2,6)
sqc12902	P4232	208	cubic	{7,3}	36	(2,6)
sqc12903	F-43m	216	cubic	{6,4,4,3,6}	38	(5,6)
sqc12904	F-43m	216	cubic	{6,4,4,4,3}	38	(5,6)
sqc12905	F-43m	216	cubic	{6,4,3,4,6}	38	(5,6)
sqc12906	F-43m	216	cubic	{4,4,6,4,3}	38	(5,6)
sqc12907	I213	199	cubic	{4,4,6,4,3}	38	(5,7)
sqc12908	I213	199	cubic	{6,4,4,3,6}	38	(5,7)
sqc12909	I213	199	cubic	{6,4,4,4,3}	38	(5,7)
sqc12910	I213	199	cubic	{6,4,3,4,6}	38	(5,7)
sqc12911	P4232	208	cubic	{6,4,4,3,6}	38	(5,6)
sqc12912	P4232	208	cubic	{6,4,4,4,3}	38	(5,6)
sqc12913	P4232	208	cubic	{4,3,4,4,6}	40	(5,6)
sqc12914	P4232	208	cubic	{6,4,3,4,6}	38	(5,6)
sqc12915	F-43m	216	cubic	{4,4,6,4,3}	38	(5,6)
sqc12916	I213	199	cubic	{4,4,6,4,3}	38	(5,7)
sqc12917	P4232	208	cubic	{4,4,6,4,3}	38	(5,6)
sqc12918	I213	199	cubic	{4,3,6,4,6}	38	(5,7)
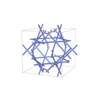
sqc12919	F-43m	216	cubic	{4,3,6,4,6}	38	(5,6)
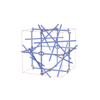
sqc12920	P4232	208	cubic	{4,3,6,4,6}	38	(5,6)
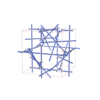
sqc12921	P4232	208	cubic	{3,4,6,4,4}	40	(5,6)
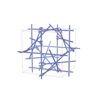
sqc12922	P4232	208	cubic	{3,4,4,4,6}	40	(5,6)
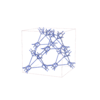
sqc12923	P4232	208	cubic	{3,4,4,6,4}	40	(5,6)
sqc12924	F-43m	216	cubic	{5,4}	36	(2,6)
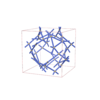
sqc12925	F-43m	216	cubic	{5,4}	36	(2,6)
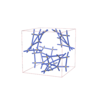
sqc12926	P4232	208	cubic	{5,4}	36	(2,6)
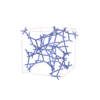
sqc12927	P4232	208	cubic	{4,5}	36	(2,6)
sqc12928	I213	199	cubic	{5,4,4}	36	(3,7)
sqc12929	I213	199	cubic	{3,5,5}	36	(3,7)
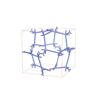
sqc12930	Fm-3m	225	cubic	{3,5}	36	(2,5)
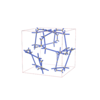
sqc12931	P4232	208	cubic	{5,3}	36	(2,6)
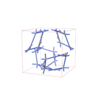
sqc12932	P4232	208	cubic	{5,3}	36	(2,6)
sqc12933	P4232	208	cubic	{5,3}	36	(2,6)
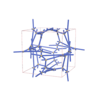
sqc12934	P4232	208	cubic	{3,5}	36	(2,6)
sqc12935	P4232	208	cubic	{5,4}	36	(2,6)
sqc12936	P4232	208	cubic	{5,4}	36	(2,6)
sqc12937	I213	199	cubic	{5,4,4}	36	(3,7)
sqc12938	P4232	208	cubic	{5,4}	36	(2,6)
sqc12939	P4232	208	cubic	{5,4}	36	(2,6)
sqc12940	P4232	208	cubic	{4,4,6,4,3}	38	(5,6)
sqc12941	P4232	208	cubic	{4,3,4,4,4}	40	(5,6)
sqc12942	P4232	208	cubic	{4,4,4,3,4}	40	(5,6)
sqc12943	I41/acd	142	tetragonal	{16,3,3}	36	(3,6)
sqc12944	I41/acd	142	tetragonal	{4,16,4}	28	(3,6)
sqc12945	I41/acd	142	tetragonal	{4,3,3,8}	44	(4,6)
sqc12946	I41/acd	142	tetragonal	{4,3,3,8}	44	(4,6)
sqc12947	I41/acd	142	tetragonal	{8,3,3}	40	(3,5)
sqc12948	I41/acd	142	tetragonal	{8,3,3}	40	(3,6)
sqc12949	I41/acd	142	tetragonal	{7,3}	32	(2,6)
sqc12950	I41/acd	142	tetragonal	{3,7}	32	(2,6)
sqc12951	I41/acd	142	tetragonal	{3,7}	32	(2,6)
sqc12952	I41/acd	142	tetragonal	{7,3}	32	(2,6)
sqc12953	I41/acd	142	tetragonal	{6,4}	32	(2,6)
sqc12954	I41/acd	142	tetragonal	{4,6}	32	(2,6)
sqc12955	I41/acd	142	tetragonal	{5,5}	32	(2,6)
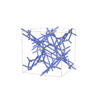
sqc12956	I41/acd	142	tetragonal	{5,5}	32	(2,6)
sqc12957	I41/acd	142	tetragonal	{5,5}	32	(2,6)
sqc12958	I41/acd	142	tetragonal	{4,4,3,4}	44	(4,6)
sqc12959	I41/acd	142	tetragonal	{4,3,4,4}	44	(4,6)
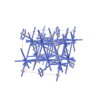
sqc12960	I41/acd	142	tetragonal	{4,3,4,4}	44	(4,6)
sqc12961	I41/acd	142	tetragonal	{4,16,4}	28	(3,6)
sqc12962	I41/acd	142	tetragonal	{6,4}	32	(2,6)
sqc12963	I41/acd	142	tetragonal	{8,3,3}	40	(3,5)
sqc12964	I41/acd	142	tetragonal	{4,8,8}	28	(3,6)
sqc12965	I41/acd	142	tetragonal	{3,12,4,4}	36	(4,5)
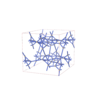
sqc12966	I41/acd	142	tetragonal	{3,12,4,4}	36	(4,5)
sqc12967	I41/acd	142	tetragonal	{4,4,8}	36	(3,6)
sqc12968	I41/acd	142	tetragonal	{4,8,8}	28	(3,6)
sqc12969	I41/acd	142	tetragonal	{4,8,6,4}	28	(4,5)
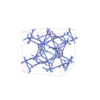
sqc12970	I41/acd	142	tetragonal	{4,8,6,4}	28	(4,5)
sqc12971	I41/acd	142	tetragonal	{8,4,4}	36	(3,5)
sqc12972	I41/acd	142	tetragonal	{8,4,4}	36	(3,5)
sqc12973	I41/acd	142	tetragonal	{3,6,4,8}	36	(4,5)
sqc12974	I41/acd	142	tetragonal	{3,6,4,8}	36	(4,5)
sqc12975	I41/acd	142	tetragonal	{3,6,8,4}	36	(4,5)
sqc12976	I41/acd	142	tetragonal	{3,6,8,4}	36	(4,5)
sqc12977	I41/acd	142	tetragonal	{7,3}	32	(2,6)
sqc12978	I41/acd	142	tetragonal	{7,3}	32	(2,6)
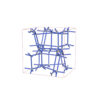
sqc12979	I41/acd	142	tetragonal	{3,7}	32	(2,6)
sqc12980	I41/acd	142	tetragonal	{3,7}	32	(2,6)
sqc12981	I41/acd	142	tetragonal	{4,4,6,4}	36	(4,5)
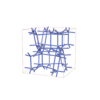
sqc12982	I41/acd	142	tetragonal	{6,4}	32	(2,6)
sqc12983	I41/acd	142	tetragonal	{4,6}	32	(2,6)
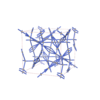
sqc12984	I41/acd	142	tetragonal	{6,4}	32	(2,6)
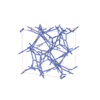
sqc12985	I41/acd	142	tetragonal	{4,4,6,4}	36	(4,5)
sqc12986	I41/acd	142	tetragonal	{3,6,4,4}	40	(4,5)
sqc12987	I41/acd	142	tetragonal	{3,6,4,4}	40	(4,5)
sqc12988	I41/acd	142	tetragonal	{5,5}	32	(2,6)
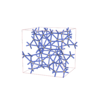
sqc12989	I41/acd	142	tetragonal	{5,5}	32	(2,6)
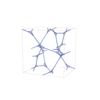
sqc12990	I41/acd	142	tetragonal	{5,5}	32	(2,6)
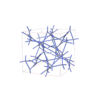
sqc12991	I41/acd	142	tetragonal	{4,4,4}	40	(3,6)
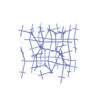
sqc12992	I41/acd	142	tetragonal	{4,3,4,4}	44	(4,6)
sqc12993	I41/acd	142	tetragonal	{4,3,4,4}	44	(4,6)
sqc12994	I41/acd	142	tetragonal	{3,4,4,4}	44	(4,6)
sqc12995	I41/acd	142	tetragonal	{3,4,4,4}	44	(4,6)
sqc12996	I41/acd	142	tetragonal	{4,4,4}	40	(3,5)
sqc12997	I41/acd	142	tetragonal	{4,4,4}	40	(3,5)
sqc12998	I41/acd	142	tetragonal	{4,4,4}	40	(3,5)
sqc12999	I41/acd	142	tetragonal	{4,4,4}	40	(3,5)