s-net search

Glossary of terms

s-net name	e.g. sqc5432
Other name
Symmetry class
Space group
Vertex transitivity
Edge transitivity
Vertices per primitive unit cell
Vertex degree(s)
Coordination sequence	any subsequence separated by spaces e.g. 4 12 30
Shortest cycle

14646 records listed.

s-net name	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
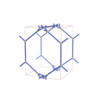
sqc4600	P-42m	111	tetragonal	{4,4,8,4}	10	(4,5)
sqc4601	Pmmm	47	orthorhombic	{3,4,7,4}	10	(4,6)
sqc4602	Imma	74	orthorhombic	{4,6,4,4}	10	(4,6)
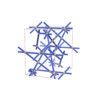
sqc4603	C2/c	15	monoclinic	{4,6,4,4}	10	(4,7)
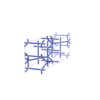
sqc4604	C2/c	15	monoclinic	{4,6,4,4}	10	(4,7)
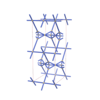
sqc4605	Imma	74	orthorhombic	{4,6,4,4}	10	(4,6)
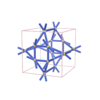
sqc4606	Cmma	67	orthorhombic	{4,4,6,4}	10	(4,5)
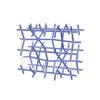
sqc4607	P4/mmm	123	tetragonal	{6,5}	8	(2,3)
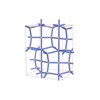
sqc4608	Cmma	67	orthorhombic	{4,4,6,4}	10	(4,5)
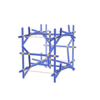
sqc4609	Cmma	67	orthorhombic	{4,4,4,6}	10	(4,5)
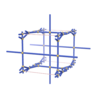
sqc4610	P4222	93	tetragonal	{4,4,4,6}	10	(4,5)
sqc4611	P42/mmc	131	tetragonal	{4,4,6,4}	10	(4,5)
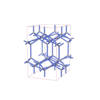
sqc4612	P42/mcm	132	tetragonal	{4,6,4,4}	10	(4,5)
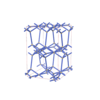
sqc4613	Fmmm	69	orthorhombic	{6,4,4,4}	10	(4,5)
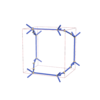
sqc4614	Fmmm	69	orthorhombic	{4,4,4,6}	10	(4,5)
sqc4615	P-4m2	115	tetragonal	{5,3}	12	(2,5)
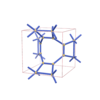
sqc4616	P-4m2	115	tetragonal	{5,3}	12	(2,5)
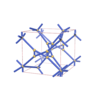
sqc4617	P4222	93	tetragonal	{5,3}	12	(2,5)
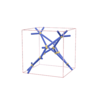
sqc4618	P4222	93	tetragonal	{5,3}	12	(2,5)
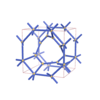
sqc4619	P4/mmm	123	tetragonal	{3,5}	12	(2,5)
sqc4620	P-42m	111	tetragonal	{5,3}	12	(2,5)
sqc4621	Fmmm	69	orthorhombic	{5,3}	12	(2,6)
sqc4622	Fmmm	69	orthorhombic	{5,3}	12	(2,6)
sqc4623	P4/mmm	123	tetragonal	{3,5}	12	(2,5)
sqc4624	P4/mmm	123	tetragonal	{3,5}	12	(2,3)
sqc4625	Imma	74	orthorhombic	{4,4,4,3,4}	12	(5,5)
sqc4626	Imma	74	orthorhombic	{4,4,4,3}	12	(4,6)
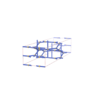
sqc4627	Imma	74	orthorhombic	{3,4,4,4}	12	(4,6)
sqc4628	Imma	74	orthorhombic	{4,3,4,4}	12	(4,6)
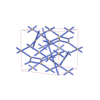
sqc4629	C2/c	15	monoclinic	{4,4,4,3,4}	12	(5,6)
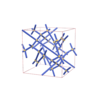
sqc4630	C2/c	15	monoclinic	{4,4,4,3}	12	(4,7)
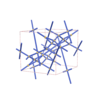
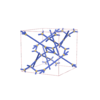
sqc4631	C2/c	15	monoclinic	{3,4,4,4}	12	(4,7)
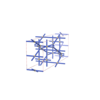
sqc4632	C2/c	15	monoclinic	{4,3,4,4}	12	(4,7)
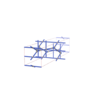
sqc4633	Imma	74	orthorhombic	{4,6,4,4}	10	(4,6)
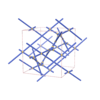
sqc4634	Imma	74	orthorhombic	{4,3,4,4}	12	(4,6)
sqc4635	C2/c	15	monoclinic	{4,3,4,4}	12	(4,7)
sqc4636	Imma	74	orthorhombic	{4,3,4,4}	12	(4,6)
sqc4637	C2/c	15	monoclinic	{4,3,4,4}	12	(4,7)
sqc4638	Imma	74	orthorhombic	{6,4,4,4}	10	(4,6)
sqc4639	Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
sqc4640	C2/c	15	monoclinic	{4,3,4,4}	12	(4,7)
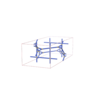
sqc4641	Imma	74	orthorhombic	{4,3,4,4}	12	(4,6)
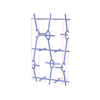
sqc4642	Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
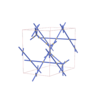
sqc4643	C2/c	15	monoclinic	{3,4,4,4}	12	(4,7)
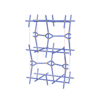
sqc4644	Imma	74	orthorhombic	{3,4,4,4}	12	(4,6)
sqc4645	Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
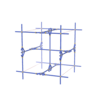
sqc4646	I4/mmm	139	tetragonal	{4,4,4,4}	11	(4,5)
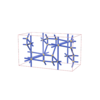
sqc4647	Cmma	67	orthorhombic	{4,6}	10	(2,5)
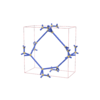
sqc4648	P-42m	111	tetragonal	{4,3}	12	(2,5)
sqc4649	P-42m	111	tetragonal	{4,3}	12	(2,5)
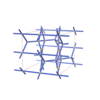
sqc4650	Cmma	67	orthorhombic	{4,4,4,6}	10	(4,6)
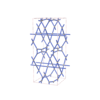
sqc4651	Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
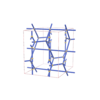
sqc4652	Fmmm	69	orthorhombic	{3,4,4,4}	12	(4,6)
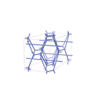
sqc4653	Cmma	67	orthorhombic	{4,4,4,3}	12	(4,6)
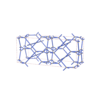
sqc4654	Fmmm	69	orthorhombic	{3,4,4,4}	12	(4,6)
sqc4655	Fmmm	69	orthorhombic	{4,4,3,4}	12	(4,6)
sqc4656	Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
sqc4657	Fmmm	69	orthorhombic	{4,4,4,6}	10	(4,5)
sqc4658	P4222	93	tetragonal	{4,3}	12	(2,5)
sqc4659	P4/mmm	123	tetragonal	{4,4,4,4}	11	(4,5)
sqc4660	Imma	74	orthorhombic	{4,4,4,6}	10	(4,6)
sqc4661	P42/mmc	131	tetragonal	{3,4}	12	(2,4)
sqc4662	P4222	93	tetragonal	{4,3}	12	(2,5)
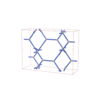
sqc4663	Cmma	67	orthorhombic	{3,4}	12	(2,5)
sqc4664	Imma	74	orthorhombic	{4,4,3,4}	12	(4,6)
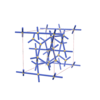
sqc4665	Imma	74	orthorhombic	{4,4,4,3}	12	(4,6)
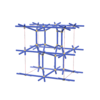
sqc4666	C2/c	15	monoclinic	{4,4,4,3}	12	(4,7)
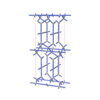
sqc4667	Cmma	67	orthorhombic	{6,4}	10	(2,5)
sqc4668	Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
sqc4669	Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
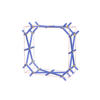
sqc4670	C2/c	15	monoclinic	{4,4,3,4}	12	(4,7)
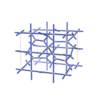
sqc4671	P4/mmm	123	tetragonal	{4,6}	10	(2,4)
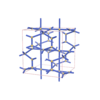
sqc4672	Cmma	67	orthorhombic	{4,4,4,3}	12	(4,6)
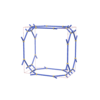
sqc4673	Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
sqc4674	P4/mmm	123	tetragonal	{4,3}	12	(2,4)
sqc4675	C2/c	15	monoclinic	{4,4,3,4}	12	(4,7)
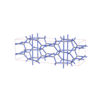
sqc4676	Fmmm	69	orthorhombic	{4,4,3,4}	12	(4,6)
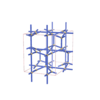
sqc4677	Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
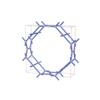
sqc4678	P4/mmm	123	tetragonal	{3,4,4}	12	(3,4)
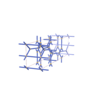
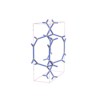
sqc4679	Imma	74	orthorhombic	{4,4,4,3}	12	(4,6)
sqc4680	Pmmm	47	orthorhombic	{3,3,3,4,3}	14	(5,6)
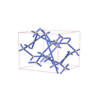
sqc4681	Pmmm	47	orthorhombic	{3,4,3,3,3}	14	(5,6)
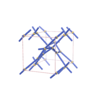
sqc4682	C2/c	15	monoclinic	{4,4,4,3}	12	(4,7)
sqc4683	P4222	93	tetragonal	{4,3}	12	(2,5)
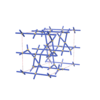
sqc4684	Imma	74	orthorhombic	{4,4,3,4,4}	12	(5,7)
sqc4685	C2/c	15	monoclinic	{4,4,3,4}	12	(4,7)
sqc4686	Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
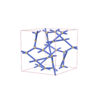
sqc4687	C2/c	15	monoclinic	{4,3,4,4}	12	(4,7)
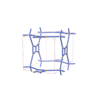
sqc4688	P42/mmc	131	tetragonal	{3,3,4}	14	(3,4)
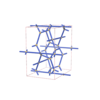
sqc4689	C2/c	15	monoclinic	{3,4,4,4}	12	(4,7)
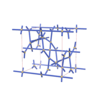
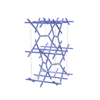
sqc4690	C2/c	15	monoclinic	{3,4,4,4}	12	(4,7)
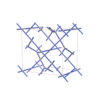
sqc4691	Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
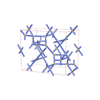
sqc4692	C2/c	15	monoclinic	{4,4,4,3}	12	(4,7)
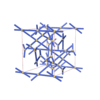
sqc4693	C2/c	15	monoclinic	{3,4,4,4}	12	(4,7)
sqc4694	C2/c	15	monoclinic	{4,4,4,3,4}	12	(5,6)
sqc4695	Imma	74	orthorhombic	{4,4,4,3,4}	12	(5,5)
sqc4696	Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
sqc4697	Imma	74	orthorhombic	{4,4,4,3}	12	(4,6)
sqc4698	Imma	74	orthorhombic	{3,4,4,4}	12	(4,6)
sqc4699	Cmma	67	orthorhombic	{6,4}	10	(2,5)