Pmmm

Number	47
Symmetry Class	orthorhombic
Chiral	N

s-nets

833 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
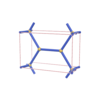
	sqc178		Pmmm	47	orthorhombic	{5,3}	4	(2,4)
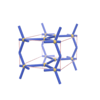
	sqc179		Pmmm	47	orthorhombic	{5,3}	4	(2,4)
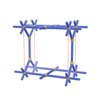
	sqc180		Pmmm	47	orthorhombic	{6,4,3}	4	(3,4)
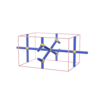
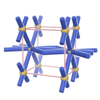
	sqc181		Pmmm	47	orthorhombic	{6,4,3}	4	(3,4)
	sqc189		Pmmm	47	orthorhombic	{4,14}	2	(2,4)
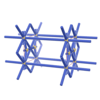
	sqc190		Pmmm	47	orthorhombic	{12,3}	3	(2,5)
	sqc191		Pmmm	47	orthorhombic	{10,4}	3	(2,5)
	sqc193		Pmmm	47	orthorhombic	{14,4}	2	(2,5)
	sqc194		Pmmm	47	orthorhombic	{6,12}	2	(2,5)
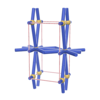
	sqc195		Pmmm	47	orthorhombic	{12,3}	3	(2,5)
	sqc196		Pmmm	47	orthorhombic	{3,12}	3	(2,5)
	sqc197		Pmmm	47	orthorhombic	{12,6}	2	(2,5)
	sqc199		Pmmm	47	orthorhombic	{12,6}	2	(2,5)
	sqc200		Pmmm	47	orthorhombic	{12,6}	2	(2,5)
	sqc201		Pmmm	47	orthorhombic	{12,3}	3	(2,5)
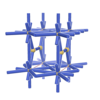
	sqc202		Pmmm	47	orthorhombic	{12,3}	3	(2,5)
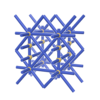
	sqc203		Pmmm	47	orthorhombic	{12,3}	3	(2,5)
	sqc204		Pmmm	47	orthorhombic	{10,4}	3	(2,6)
	sqc205		Pmmm	47	orthorhombic	{10,4}	3	(2,6)
	sqc206		Pmmm	47	orthorhombic	{8,10}	2	(2,5)
	sqc207		Pmmm	47	orthorhombic	{8,10}	2	(2,5)
	sqc208		Pmmm	47	orthorhombic	{4,10}	3	(2,5)
	sqc210		Pmmm	47	orthorhombic	{10,4}	3	(2,5)
	sqc218		Pmmm	47	orthorhombic	{4,10}	3	(2,6)
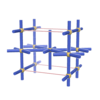
	sqc219		Pmmm	47	orthorhombic	{4,6,8}	3	(3,5)
	sqc220		Pmmm	47	orthorhombic	{4,6,8}	3	(3,5)
	sqc221		Pmmm	47	orthorhombic	{8,4,6}	3	(3,5)
	sqc222		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
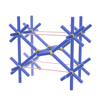
	sqc223		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
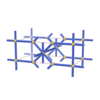
	sqc224		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
	sqc225		Pmmm	47	orthorhombic	{4,3,8}	4	(3,5)
	sqc226		Pmmm	47	orthorhombic	{3,8,4}	4	(3,5)
	sqc227		Pmmm	47	orthorhombic	{5,8}	3	(2,5)
	sqc230		Pmmm	47	orthorhombic	{7,4}	3	(2,4)
	sqc232		Pmmm	47	orthorhombic	{6,6}	3	(2,6)
	sqc233		Pmmm	47	orthorhombic	{4,7}	3	(2,4)
	sqc235		Pmmm	47	orthorhombic	{6,8,4}	3	(3,5)
	sqc236		Pmmm	47	orthorhombic	{8,6,4}	3	(3,5)
	sqc237		Pmmm	47	orthorhombic	{6,8,4}	3	(3,5)
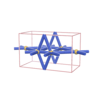
	sqc238		Pmmm	47	orthorhombic	{7,4}	3	(2,4)
	sqc239		Pmmm	47	orthorhombic	{4,3,8}	4	(3,5)
	sqc240		Pmmm	47	orthorhombic	{3,8,4}	4	(3,5)
	sqc241		Pmmm	47	orthorhombic	{4,6,8}	3	(3,4)
	sqc242		Pmmm	47	orthorhombic	{4,8,6}	3	(3,5)
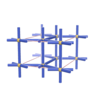
	sqc247	btu	Pmmm	47	orthorhombic	{6,6}	3	(2,5)
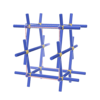
	sqc248		Pmmm	47	orthorhombic	{6,6}	3	(2,5)
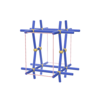
	sqc251		Pmmm	47	orthorhombic	{6,3}	4	(2,5)
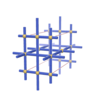
	sqc252		Pmmm	47	orthorhombic	{4,4,4,6}	4	(4,6)
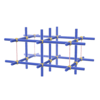
	sqc253		Pmmm	47	orthorhombic	{4,4,6,4}	4	(4,6)
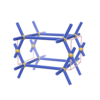
	sqc255		Pmmm	47	orthorhombic	{7,4}	3	(2,4)
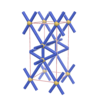
	sqc257		Pmmm	47	orthorhombic	{4,7}	3	(2,4)
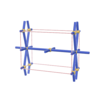
	sqc259		Pmmm	47	orthorhombic	{3,8,4}	4	(3,5)
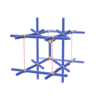
	sqc260		Pmmm	47	orthorhombic	{3,4,8}	4	(3,5)
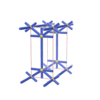
	sqc263		Pmmm	47	orthorhombic	{6,6}	3	(2,5)
	sqc265		Pmmm	47	orthorhombic	{6,6}	3	(2,5)
	sqc266		Pmmm	47	orthorhombic	{6,6}	3	(2,5)
	sqc267		Pmmm	47	orthorhombic	{4,6,4}	4	(3,5)
	sqc268		Pmmm	47	orthorhombic	{4,4,6}	4	(3,5)
	sqc269		Pmmm	47	orthorhombic	{4,4,6}	4	(3,5)
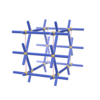
	sqc270		Pmmm	47	orthorhombic	{4,4,6}	4	(3,5)
	sqc271		Pmmm	47	orthorhombic	{4,6,4}	4	(3,5)
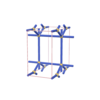
	sqc274		Pmmm	47	orthorhombic	{6,3}	4	(2,5)
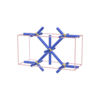
	sqc276		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
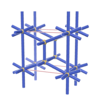
	sqc277		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
	sqc279		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
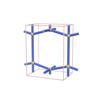
	sqc280		Pmmm	47	orthorhombic	{4,5}	4	(2,5)
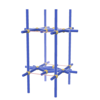
	sqc281		Pmmm	47	orthorhombic	{4,8,3}	4	(3,5)
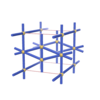
	sqc282		Pmmm	47	orthorhombic	{4,4,6}	4	(3,5)
	sqc283		Pmmm	47	orthorhombic	{6,4,4,4}	4	(4,4)
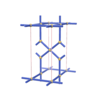
	sqc285		Pmmm	47	orthorhombic	{4,4,3,4}	5	(4,4)
	sqc286		Pmmm	47	orthorhombic	{4,3,4,4}	5	(4,4)
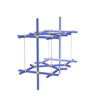
	sqc287		Pmmm	47	orthorhombic	{3,4,4,4}	5	(4,4)
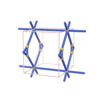
	sqc295		Pmmm	47	orthorhombic	{3,6}	5	(2,4)
	sqc297		Pmmm	47	orthorhombic	{5,4}	4	(2,5)
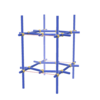
	sqc300		Pmmm	47	orthorhombic	{4,4,3}	5	(3,5)
	sqc301		Pmmm	47	orthorhombic	{4,4,3}	5	(3,5)
	sqc303		Pmmm	47	orthorhombic	{3,4,4}	5	(3,5)
	sqc304		Pmmm	47	orthorhombic	{3,8,4}	4	(3,5)
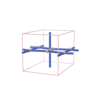
	sqc305		Pmmm	47	orthorhombic	{4,3,4}	5	(3,5)
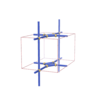
	sqc308		Pmmm	47	orthorhombic	{3,4,4}	5	(3,5)
	sqc309		Pmmm	47	orthorhombic	{4,6,8}	3	(3,5)
	sqc310		Pmmm	47	orthorhombic	{4,4,6,4}	4	(4,4)
	sqc311		Pmmm	47	orthorhombic	{4,4,6,4}	4	(4,4)
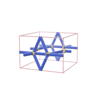
	sqc312		Pmmm	47	orthorhombic	{6,3}	4	(2,5)
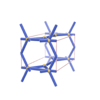
	sqc319		Pmmm	47	orthorhombic	{6,3}	4	(2,5)
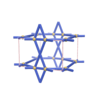
	sqc322		Pmmm	47	orthorhombic	{4,5}	4	(2,5)
	sqc323		Pmmm	47	orthorhombic	{4,6,4}	4	(3,5)
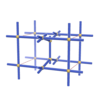
	sqc324		Pmmm	47	orthorhombic	{4,4,6}	4	(3,5)
	sqc329		Pmmm	47	orthorhombic	{6,14}	2	(2,5)
	sqc330		Pmmm	47	orthorhombic	{16,4}	2	(2,5)
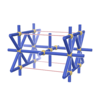
	sqc332		Pmmm	47	orthorhombic	{4,8,4,4}	4	(4,6)
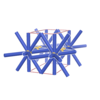
	sqc333		Pmmm	47	orthorhombic	{4,12}	3	(2,6)
	sqc335		Pmmm	47	orthorhombic	{14,3}	3	(2,6)
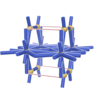
	sqc336		Pmmm	47	orthorhombic	{14,3}	3	(2,6)
	sqc337		Pmmm	47	orthorhombic	{3,14}	3	(2,6)
	sqc338		Pmmm	47	orthorhombic	{3,14}	3	(2,5)
	sqc339		Pmmm	47	orthorhombic	{12,4}	3	(2,6)
	sqc340		Pmmm	47	orthorhombic	{12,4}	3	(2,6)
	sqc343		Pmmm	47	orthorhombic	{5,10}	3	(2,5)
	sqc344		Pmmm	47	orthorhombic	{10,5}	3	(2,5)