Pmmm

Number	47
Symmetry Class	orthorhombic
Chiral	N

s-nets

833 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
	sqc1021		Pmmm	47	orthorhombic	{6,7}	4	(2,7)
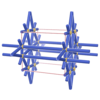
	sqc1024		Pmmm	47	orthorhombic	{6,7}	4	(2,7)
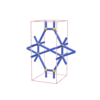
	sqc1025		Pmmm	47	orthorhombic	{3,7}	6	(2,6)
	sqc1026		Pmmm	47	orthorhombic	{3,7}	6	(2,6)
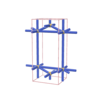
	sqc1030		Pmmm	47	orthorhombic	{8,5}	4	(2,7)
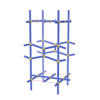
	sqc1031		Pmmm	47	orthorhombic	{4,4,4,3,4}	7	(5,7)
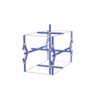
	sqc1032		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
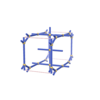
	sqc1033		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
	sqc1034		Pmmm	47	orthorhombic	{4,4,4,8,6}	5	(5,6)
	sqc1035		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
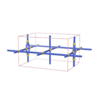
	sqc1036		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
	sqc1037		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
	sqc1038		Pmmm	47	orthorhombic	{4,4,4,4,3}	7	(5,7)
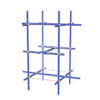
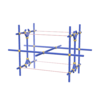
	sqc1039		Pmmm	47	orthorhombic	{4,3,4,4,4}	7	(5,7)
	sqc1040		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
	sqc1041		Pmmm	47	orthorhombic	{4,4,4,3,4}	7	(5,7)
	sqc1043		Pmmm	47	orthorhombic	{4,4,4,4,3}	7	(5,7)
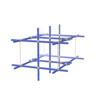
	sqc1044		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
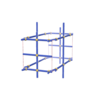
	sqc1045		Pmmm	47	orthorhombic	{4,3,4,4,4}	7	(5,7)
	sqc1046		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
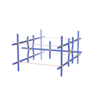
	sqc1048		Pmmm	47	orthorhombic	{4,6,4,4,4}	6	(5,6)
	sqc1049		Pmmm	47	orthorhombic	{4,4,4,4,3}	7	(5,7)
	sqc1050		Pmmm	47	orthorhombic	{4,6,4,4,4}	6	(5,6)
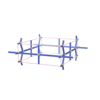
	sqc1051		Pmmm	47	orthorhombic	{6,4,4,4,4}	6	(5,6)
	sqc1052		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
	sqc1054		Pmmm	47	orthorhombic	{4,3,4,4,4}	7	(5,7)
	sqc1055		Pmmm	47	orthorhombic	{4,4,3,4,4}	7	(5,7)
	sqc1056		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
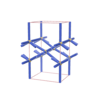
	sqc1057		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,7)
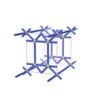
	sqc1061		Pmmm	47	orthorhombic	{7,6}	4	(2,5)
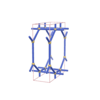
	sqc1064		Pmmm	47	orthorhombic	{6,5}	5	(2,6)
	sqc1070		Pmmm	47	orthorhombic	{3,5}	6	(2,5)
	sqc1073		Pmmm	47	orthorhombic	{4,5}	6	(2,6)
	sqc1075		Pmmm	47	orthorhombic	{4,5}	6	(2,6)
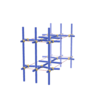
	sqc1076		Pmmm	47	orthorhombic	{4,5}	6	(2,6)
	sqc1078		Pmmm	47	orthorhombic	{4,4,3,4,4}	7	(5,7)
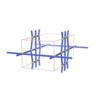
	sqc1079		Pmmm	47	orthorhombic	{4,4,4,4,6}	6	(5,6)
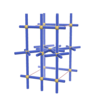
	sqc1080		Pmmm	47	orthorhombic	{3,4,4,4,4}	7	(5,6)
	sqc1088		Pmmm	47	orthorhombic	{4,8,6,4,4}	5	(5,6)
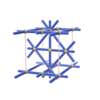
	sqc1089		Pmmm	47	orthorhombic	{4,4,6,8,4}	5	(5,6)
	sqc1090		Pmmm	47	orthorhombic	{4,4,8,6,4}	5	(5,6)
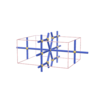
	sqc1091		Pmmm	47	orthorhombic	{4,8,6,4,4}	5	(5,6)
	sqc1095		Pmmm	47	orthorhombic	{4,8,3,4,4}	6	(5,6)
	sqc1096		Pmmm	47	orthorhombic	{4,8,3,4,4}	6	(5,6)
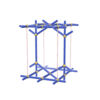
	sqc1104		Pmmm	47	orthorhombic	{5,4}	6	(2,6)
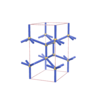
	sqc1107		Pmmm	47	orthorhombic	{4,4,4,6,4}	6	(5,6)
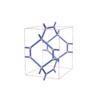
	sqc1109		Pmmm	47	orthorhombic	{5,4}	6	(2,4)
	sqc1119		Pmmm	47	orthorhombic	{3,4,3}	8	(3,5)
	sqc1122		Pmmm	47	orthorhombic	{3,16}	5	(2,7)
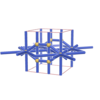
	sqc1129		Pmmm	47	orthorhombic	{4,12}	5	(2,7)
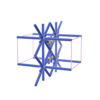
	sqc1131		Pmmm	47	orthorhombic	{4,12}	5	(2,7)
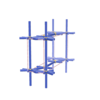
	sqc1137		Pmmm	47	orthorhombic	{9,5}	4	(2,7)
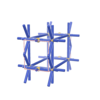
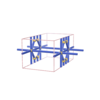
	sqc1146		Pmmm	47	orthorhombic	{9,5}	4	(2,7)
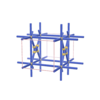
	sqc1149		Pmmm	47	orthorhombic	{3,8}	6	(2,7)
	sqc1150		Pmmm	47	orthorhombic	{8,3}	6	(2,7)
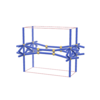
	sqc1155		Pmmm	47	orthorhombic	{5,8}	5	(2,7)
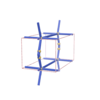
	sqc1163		Pmmm	47	orthorhombic	{8,3}	6	(2,7)
	sqc1176		Pmmm	47	orthorhombic	{8,3}	6	(2,7)
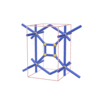
	sqc1177		Pmmm	47	orthorhombic	{3,8}	6	(2,7)
	sqc1182		Pmmm	47	orthorhombic	{8,3}	6	(2,7)
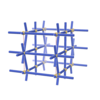
	sqc1183		Pmmm	47	orthorhombic	{3,8}	6	(2,7)
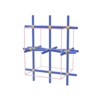
	sqc1187		Pmmm	47	orthorhombic	{4,4,4,4,8}	6	(5,7)
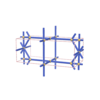
	sqc1195		Pmmm	47	orthorhombic	{4,4,8,4,4}	6	(5,7)
	sqc1201		Pmmm	47	orthorhombic	{4,4,4,4,8}	6	(5,7)
	sqc1202		Pmmm	47	orthorhombic	{4,4,8,4,4}	6	(5,7)
	sqc1203		Pmmm	47	orthorhombic	{4,4,4,8,4}	6	(5,7)
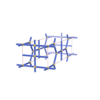
	sqc1211		Pmmm	47	orthorhombic	{6,4}	5	(2,5)
	sqc1215		Pmmm	47	orthorhombic	{3,4,3,4,4,4}	8	(6,7)
	sqc1216		Pmmm	47	orthorhombic	{4,4,4,4,8}	6	(5,7)
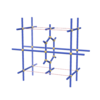
	sqc1217		Pmmm	47	orthorhombic	{8,4,4,4,4}	6	(5,7)
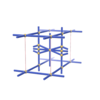
	sqc1218		Pmmm	47	orthorhombic	{4,4,4,3,3,4}	8	(6,7)
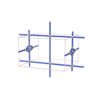
	sqc1220		Pmmm	47	orthorhombic	{4,4,4,8,4}	6	(5,7)
	sqc1221		Pmmm	47	orthorhombic	{4,4,4,4,4}	7	(5,7)
	sqc1222		Pmmm	47	orthorhombic	{4,4,4,4,4}	7	(5,7)
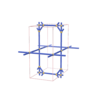
	sqc1223		Pmmm	47	orthorhombic	{4,4,4,4,4}	7	(5,7)
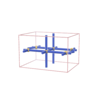
	sqc1227		Pmmm	47	orthorhombic	{4,6}	6	(2,7)
	sqc1259		Pmmm	47	orthorhombic	{4,4,4,4,4}	7	(5,7)
	sqc1262		Pmmm	47	orthorhombic	{4,4,4,4,4}	7	(5,7)
	sqc1295		Pmmm	47	orthorhombic	{4,4,4,4,8}	6	(5,7)
	sqc1303		Pmmm	47	orthorhombic	{7,4,3}	6	(3,4)
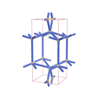
	sqc1304		Pmmm	47	orthorhombic	{5,6,3}	6	(3,4)
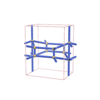
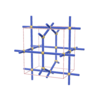
	sqc1323		Pmmm	47	orthorhombic	{4,6}	6	(2,5)
	sqc1325		Pmmm	47	orthorhombic	{3,4,4,6,4,4}	7	(6,6)
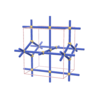
	sqc1326		Pmmm	47	orthorhombic	{6,3,4,4,4,4}	7	(6,6)
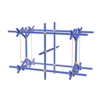
	sqc1327		Pmmm	47	orthorhombic	{3,4,4,4,4,6}	7	(6,6)
	sqc1341		Pmmm	47	orthorhombic	{8,4,4,4,4}	6	(5,7)
	sqc1342		Pmmm	47	orthorhombic	{4,4,4,4,8}	6	(5,7)
	sqc1343		Pmmm	47	orthorhombic	{4,4,8,4,4}	6	(5,7)
	sqc1344		Pmmm	47	orthorhombic	{4,8,4,4,4}	6	(5,7)
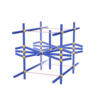
	sqc1345		Pmmm	47	orthorhombic	{4,4,4,4,8}	6	(5,7)
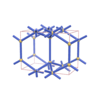
	sqc1346		Pmmm	47	orthorhombic	{4,4,4,8,4}	6	(5,7)
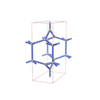
	sqc1353		Pmmm	47	orthorhombic	{3,6,5}	6	(3,4)
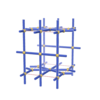
	sqc1355		Pmmm	47	orthorhombic	{5,3,3}	8	(3,4)
	sqc1391		Pmmm	47	orthorhombic	{3,4,4,6,4,4}	7	(6,6)
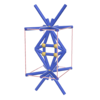
	sqc1419		Pmmm	47	orthorhombic	{3,3,5}	8	(3,4)
	sqc1447		Pmmm	47	orthorhombic	{4,14}	5	(2,7)
	sqc1460		Pmmm	47	orthorhombic	{9,3}	6	(2,7)
	sqc1461		Pmmm	47	orthorhombic	{9,3}	6	(2,7)
	sqc1471		Pmmm	47	orthorhombic	{7,4}	6	(2,7)
	sqc1473		Pmmm	47	orthorhombic	{4,7}	6	(2,7)