Pmmm

Number	47
Symmetry Class	orthorhombic
Chiral	N

s-nets

833 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
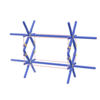
	sqc714		Pmmm	47	orthorhombic	{3,12}	5	(2,6)
	sqc716		Pmmm	47	orthorhombic	{3,12}	5	(2,6)
	sqc727		Pmmm	47	orthorhombic	{4,10}	3	(2,6)
	sqc728		Pmmm	47	orthorhombic	{6,9}	3	(2,6)
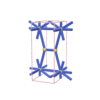
	sqc729		Pmmm	47	orthorhombic	{9,3}	4	(2,6)
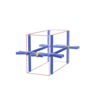
	sqc730		Pmmm	47	orthorhombic	{9,3}	4	(2,6)
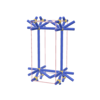
	sqc731		Pmmm	47	orthorhombic	{10,4}	3	(2,6)
	sqc732		Pmmm	47	orthorhombic	{3,9}	4	(2,6)
	sqc733		Pmmm	47	orthorhombic	{8,4}	4	(2,7)
	sqc742		Pmmm	47	orthorhombic	{10,4}	3	(2,6)
	sqc743		Pmmm	47	orthorhombic	{9,6}	3	(2,6)
	sqc744		Pmmm	47	orthorhombic	{9,3}	4	(2,6)
	sqc748		Pmmm	47	orthorhombic	{4,8}	4	(2,7)
	sqc749		Pmmm	47	orthorhombic	{5,7}	4	(2,6)
	sqc752		Pmmm	47	orthorhombic	{4,8}	5	(2,6)
	sqc753		Pmmm	47	orthorhombic	{4,8}	5	(2,6)
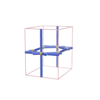
	sqc754		Pmmm	47	orthorhombic	{4,8}	5	(2,6)
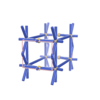
	sqc755		Pmmm	47	orthorhombic	{4,8}	5	(2,6)
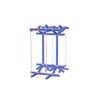
	sqc761		Pmmm	47	orthorhombic	{7,5}	4	(2,6)
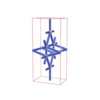
	sqc762		Pmmm	47	orthorhombic	{7,5}	4	(2,6)
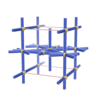
	sqc766		Pmmm	47	orthorhombic	{5,7}	4	(2,6)
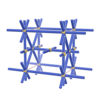
	sqc769		Pmmm	47	orthorhombic	{4,4,8,8}	4	(4,6)
	sqc770		Pmmm	47	orthorhombic	{8,8,4,4}	4	(4,6)
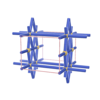
	sqc771		Pmmm	47	orthorhombic	{8,8,4,4}	4	(4,6)
	sqc773		Pmmm	47	orthorhombic	{8,4}	4	(2,7)
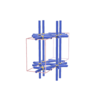
	sqc777		Pmmm	47	orthorhombic	{4,4,8,4}	5	(4,6)
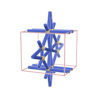
	sqc781		Pmmm	47	orthorhombic	{7,5}	4	(2,6)
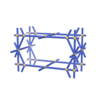
	sqc782		Pmmm	47	orthorhombic	{7,5}	4	(2,6)
	sqc790		Pmmm	47	orthorhombic	{4,4,4,8}	5	(4,6)
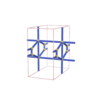
	sqc791		Pmmm	47	orthorhombic	{4,4,8,4}	5	(4,6)
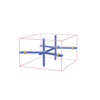
	sqc801		Pmmm	47	orthorhombic	{3,6}	6	(2,6)
	sqc802		Pmmm	47	orthorhombic	{3,6}	6	(2,6)
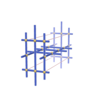
	sqc803		Pmmm	47	orthorhombic	{3,6}	6	(2,6)
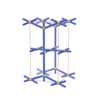
	sqc804		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,7)
	sqc805		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,6)
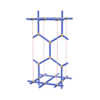
	sqc806		Pmmm	47	orthorhombic	{3,4,4,6,4}	6	(5,6)
	sqc807		Pmmm	47	orthorhombic	{4,4,3,4,3}	7	(5,6)
	sqc808		Pmmm	47	orthorhombic	{3,3,4,4,4}	7	(5,6)
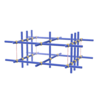
	sqc809		Pmmm	47	orthorhombic	{4,8,4,4}	5	(4,6)
	sqc810		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,7)
	sqc811		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,6)
	sqc812		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,7)
	sqc813		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,7)
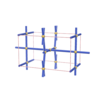
	sqc814		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,6)
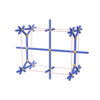
	sqc815		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,6)
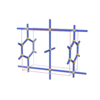
	sqc816		Pmmm	47	orthorhombic	{3,4,6,4,4}	6	(5,6)
	sqc817		Pmmm	47	orthorhombic	{3,4,3,4,4}	7	(5,6)
	sqc818		Pmmm	47	orthorhombic	{3,4,6,4,4}	6	(5,6)
	sqc819		Pmmm	47	orthorhombic	{3,4,4,4,6}	6	(5,6)
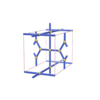
	sqc820		Pmmm	47	orthorhombic	{4,4,3,3,4}	7	(5,6)
	sqc821		Pmmm	47	orthorhombic	{3,4,3,4,4}	7	(5,6)
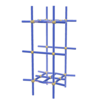
	sqc822		Pmmm	47	orthorhombic	{4,4,4,3,3}	7	(5,6)
	sqc823		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,7)
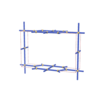
	sqc824		Pmmm	47	orthorhombic	{4,4,4,4}	6	(4,7)
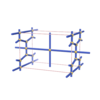
	sqc827		Pmmm	47	orthorhombic	{3,4,4,3,4}	7	(5,6)
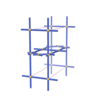
	sqc828		Pmmm	47	orthorhombic	{4,4,4,3,3}	7	(5,6)
	sqc829		Pmmm	47	orthorhombic	{4,4,4,4,4}	6	(5,6)
	sqc830		Pmmm	47	orthorhombic	{3,4,4,3,4}	7	(5,6)
	sqc831		Pmmm	47	orthorhombic	{4,3,4,4,3}	7	(5,6)
	sqc832		Pmmm	47	orthorhombic	{4,4,4,3,3}	7	(5,6)
	sqc833		Pmmm	47	orthorhombic	{3,3,4,4,4}	7	(5,6)
	sqc835		Pmmm	47	orthorhombic	{5,7}	4	(2,4)
	sqc838		Pmmm	47	orthorhombic	{6,6}	4	(2,7)
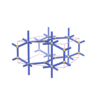
	sqc839		Pmmm	47	orthorhombic	{5,7}	4	(2,4)
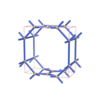
	sqc844		Pmmm	47	orthorhombic	{3,6,3}	6	(3,5)
	sqc846		Pmmm	47	orthorhombic	{5,4,3}	6	(3,5)
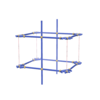
	sqc855		Pmmm	47	orthorhombic	{4,8,4,4}	5	(4,6)
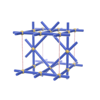
	sqc858		Pmmm	47	orthorhombic	{4,4,4,4}	6	(4,6)
	sqc881		Pmmm	47	orthorhombic	{4,4,6,6,4}	5	(5,5)
	sqc883		Pmmm	47	orthorhombic	{4,8,8,4}	4	(4,6)
	sqc901		Pmmm	47	orthorhombic	{3,6}	6	(2,6)
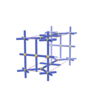
	sqc919		Pmmm	47	orthorhombic	{3,4,4,6,4}	6	(5,6)
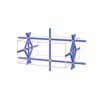
	sqc920		Pmmm	47	orthorhombic	{6,4,4,3,4}	6	(5,6)
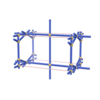
	sqc926		Pmmm	47	orthorhombic	{4,4,8,4}	5	(4,6)
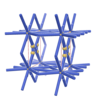
	sqc927		Pmmm	47	orthorhombic	{4,4,8,4}	5	(4,6)
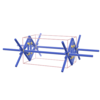
	sqc979		Pmmm	47	orthorhombic	{14,3}	5	(2,6)
	sqc980		Pmmm	47	orthorhombic	{4,10}	5	(2,6)
	sqc981		Pmmm	47	orthorhombic	{14,3}	5	(2,7)
	sqc982		Pmmm	47	orthorhombic	{10,4}	5	(2,6)
	sqc983		Pmmm	47	orthorhombic	{10,4}	5	(2,6)
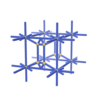
	sqc985		Pmmm	47	orthorhombic	{3,14}	5	(2,7)
	sqc989		Pmmm	47	orthorhombic	{10,4}	5	(2,7)
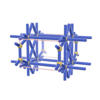
	sqc990		Pmmm	47	orthorhombic	{10,3}	4	(2,7)
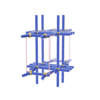
	sqc991		Pmmm	47	orthorhombic	{3,10}	4	(2,7)
	sqc992		Pmmm	47	orthorhombic	{4,9}	4	(2,7)
	sqc993		Pmmm	47	orthorhombic	{3,10}	4	(2,7)
	sqc994		Pmmm	47	orthorhombic	{10,3}	4	(2,7)
	sqc995		Pmmm	47	orthorhombic	{4,9}	4	(2,7)
	sqc997		Pmmm	47	orthorhombic	{10,3}	4	(2,7)
	sqc1000		Pmmm	47	orthorhombic	{3,7}	6	(2,6)
	sqc1002		Pmmm	47	orthorhombic	{8,5}	4	(2,7)
	sqc1003		Pmmm	47	orthorhombic	{7,6}	4	(2,7)
	sqc1004		Pmmm	47	orthorhombic	{3,7}	6	(2,6)
	sqc1006		Pmmm	47	orthorhombic	{8,4,4,4,6}	5	(5,6)
	sqc1007		Pmmm	47	orthorhombic	{8,4,4,4,6}	5	(5,6)
	sqc1008		Pmmm	47	orthorhombic	{4,6,8,4,4}	5	(5,6)
	sqc1011		Pmmm	47	orthorhombic	{5,8}	4	(2,7)
	sqc1014		Pmmm	47	orthorhombic	{7,3}	6	(2,6)
	sqc1015		Pmmm	47	orthorhombic	{5,8}	4	(2,5)
	sqc1019		Pmmm	47	orthorhombic	{8,5}	4	(2,5)