Pmmm

Number	47
Symmetry Class	orthorhombic
Chiral	N

s-nets

833 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
	sqc3000		Pmmm	47	orthorhombic	{3,4,3,5}	10	(4,5)
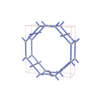
	sqc3029		Pmmm	47	orthorhombic	{3,4,4,3}	10	(4,6)
	sqc3065		Pmmm	47	orthorhombic	{5,7}	6	(2,6)
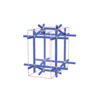
	sqc3066		Pmmm	47	orthorhombic	{7,5}	6	(2,6)
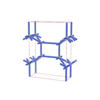
	sqc3067		Pmmm	47	orthorhombic	{7,6}	6	(2,6)
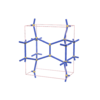
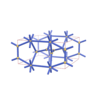
	sqc3074		Pmmm	47	orthorhombic	{5,4,3,3}	10	(4,6)
	sqc3075		Pmmm	47	orthorhombic	{3,7,3,3}	10	(4,6)
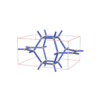
	sqc3077		Pmmm	47	orthorhombic	{4,4,4,3}	10	(4,5)
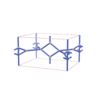
	sqc3078		Pmmm	47	orthorhombic	{4,4,3}	10	(3,6)
	sqc3082		Pmmm	47	orthorhombic	{6,3,4,3}	10	(4,6)
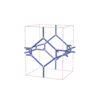
	sqc3084		Pmmm	47	orthorhombic	{7,3,3,3}	10	(4,6)
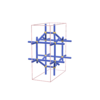
	sqc3086		Pmmm	47	orthorhombic	{4,4,3}	10	(3,6)
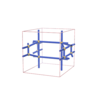
	sqc3235		Pmmm	47	orthorhombic	{6,4}	8	(2,6)
	sqc3410		Pmmm	47	orthorhombic	{4,6}	8	(2,7)
	sqc3423		Pmmm	47	orthorhombic	{4,4,4,4,4,4,4,4}	10	(8,9)
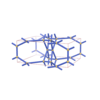
	sqc3532		Pmmm	47	orthorhombic	{3,4,6,3}	10	(4,6)
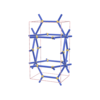
	sqc3541		Pmmm	47	orthorhombic	{3,4,4,5}	10	(4,6)
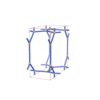
	sqc3550		Pmmm	47	orthorhombic	{3,8,3,3}	10	(4,6)
	sqc3706		Pmmm	47	orthorhombic	{3,4,3,3}	12	(4,6)
	sqc3709		Pmmm	47	orthorhombic	{3,4,3,3}	12	(4,6)
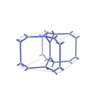
	sqc3788		Pmmm	47	orthorhombic	{4,6,3,3}	10	(4,6)
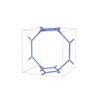
	sqc3796		Pmmm	47	orthorhombic	{5,4,4,3}	10	(4,6)
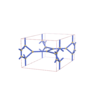
	sqc3822		Pmmm	47	orthorhombic	{4,3,3,3}	12	(4,6)
	sqc3839		Pmmm	47	orthorhombic	{3,4,3,3}	12	(4,6)
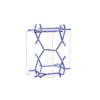
	sqc3849		Pmmm	47	orthorhombic	{3,3,4,4,3}	12	(5,7)
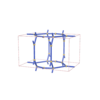
	sqc3850		Pmmm	47	orthorhombic	{3,4,3,3}	12	(4,6)
	sqc3874		Pmmm	47	orthorhombic	{4,3,3,3}	12	(4,6)
	sqc3940		Pmmm	47	orthorhombic	{7,6,4,4}	8	(4,5)
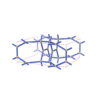
	sqc3954		Pmmm	47	orthorhombic	{3,4,4,3}	12	(4,6)
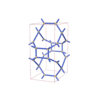
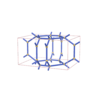
	sqc3992		Pmmm	47	orthorhombic	{4,3,4,3}	12	(4,6)
	sqc3994		Pmmm	47	orthorhombic	{3,4,4,3}	12	(4,6)
	sqc4082		Pmmm	47	orthorhombic	{4,7}	8	(2,7)
	sqc4091		Pmmm	47	orthorhombic	{7,4}	8	(2,7)
	sqc4092		Pmmm	47	orthorhombic	{7,4}	8	(2,7)
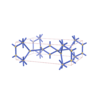
	sqc4140		Pmmm	47	orthorhombic	{6,5}	8	(2,7)
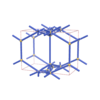
	sqc4362		Pmmm	47	orthorhombic	{3,6,3,4,3}	12	(5,6)
	sqc4382		Pmmm	47	orthorhombic	{3,8,7,4}	8	(4,6)
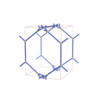
	sqc4480		Pmmm	47	orthorhombic	{3,4,4,4,3}	12	(5,6)
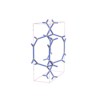
	sqc4601		Pmmm	47	orthorhombic	{3,4,7,4}	10	(4,6)
	sqc4680		Pmmm	47	orthorhombic	{3,3,3,4,3}	14	(5,6)
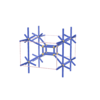
	sqc4681		Pmmm	47	orthorhombic	{3,4,3,3,3}	14	(5,6)
	sqc4721		Pmmm	47	orthorhombic	{7,4}	10	(2,6)
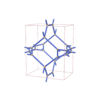
	sqc4726		Pmmm	47	orthorhombic	{4,7,4,4}	10	(4,6)
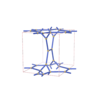
	sqc4732		Pmmm	47	orthorhombic	{4,4,4,3}	12	(4,7)
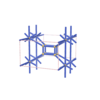
	sqc4734		Pmmm	47	orthorhombic	{3,4,3,3,3}	14	(5,7)
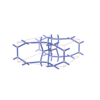
	sqc4815		Pmmm	47	orthorhombic	{8,4}	10	(2,7)
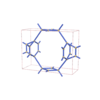
	sqc5303		Pmmm	47	orthorhombic	{3,4,4,3,3}	14	(5,7)
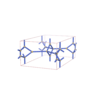
	sqc5304		Pmmm	47	orthorhombic	{3,4,4,3,3}	14	(5,7)
	sqc5514		Pmmm	47	orthorhombic	{3,4,3,4,3}	14	(5,7)
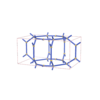
	sqc5539		Pmmm	47	orthorhombic	{3,4,3,4,3}	14	(5,7)
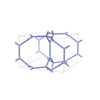
	sqc5540		Pmmm	47	orthorhombic	{3,3,4,4,3}	14	(5,7)
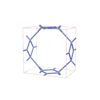
	sqc5541		Pmmm	47	orthorhombic	{4,3,3,4,3}	14	(5,7)
	sqc5612		Pmmm	47	orthorhombic	{3,8,6,4,4}	10	(5,6)
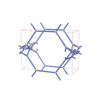
	sqc5613		Pmmm	47	orthorhombic	{7,6,4,4,4}	10	(5,6)
	sqc5614		Pmmm	47	orthorhombic	{3,4,6,4,4}	12	(5,6)
	sqc5615		Pmmm	47	orthorhombic	{7,3,4,4,4}	12	(5,6)
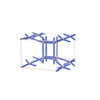
	sqc5616		Pmmm	47	orthorhombic	{5,5}	10	(2,6)
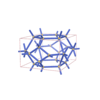
	sqc5797		Pmmm	47	orthorhombic	{4,6,4,4,4}	12	(5,6)
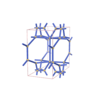
	sqc5812		Pmmm	47	orthorhombic	{3,4,7,4,4}	12	(5,7)
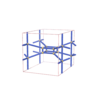
	sqc5940		Pmmm	47	orthorhombic	{5,4}	12	(2,7)
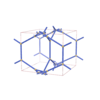
	sqc5992		Pmmm	47	orthorhombic	{3,4,8,4,3}	12	(5,7)
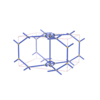
	sqc5995		Pmmm	47	orthorhombic	{3,4,4,7,4}	12	(5,7)
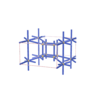
	sqc6141		Pmmm	47	orthorhombic	{7,5}	10	(2,7)
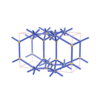
	sqc6167		Pmmm	47	orthorhombic	{3,8,4,4,4}	12	(5,7)
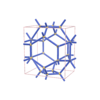
	sqc6170		Pmmm	47	orthorhombic	{4,7,4,4,4}	12	(5,7)
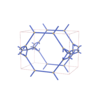
	sqc6217		Pmmm	47	orthorhombic	{3,4,4,4,4}	14	(5,7)
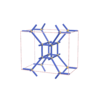
	sqc6702		Pmmm	47	orthorhombic	{4,5}	12	(2,7)
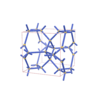
	sqc6801		Pmmm	47	orthorhombic	{3,6,4,4,4,4}	14	(6,6)
	sqc6981		Pmmm	47	orthorhombic	{5,6}	10	(2,7)
	sqc6982		Pmmm	47	orthorhombic	{3,4,4,6,4,4}	14	(6,7)
	sqc6983		Pmmm	47	orthorhombic	{3,4,6,4,4,4}	14	(6,7)
	sqc6984		Pmmm	47	orthorhombic	{3,8,3,4,4,4}	14	(6,7)
	sqc6985		Pmmm	47	orthorhombic	{3,4,3,4,4,4}	16	(6,7)
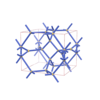
	sqc6986		Pmmm	47	orthorhombic	{7,3,4,4,4,4}	14	(6,7)
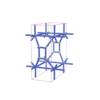
	sqc7019		Pmmm	47	orthorhombic	{7,4}	12	(2,8)
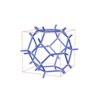
	sqc7277		Pmmm	47	orthorhombic	{4,6,4,4,4,4}	14	(6,7)
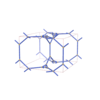
	sqc7349		Pmmm	47	orthorhombic	{3,4,4,4,4,3}	16	(6,8)
	sqc7379		Pmmm	47	orthorhombic	{4,3,4,4,4,4}	16	(6,7)
	sqc7395		Pmmm	47	orthorhombic	{3,4,4,4,4,4}	16	(6,8)
	sqc7396		Pmmm	47	orthorhombic	{3,4,4,4,4,4}	16	(6,8)
	sqc7576		Pmmm	47	orthorhombic	{4,6}	12	(2,8)
	sqc8215		Pmmm	47	orthorhombic	{3,4,4,3,4,4,4}	18	(7,8)
	sqc8258		Pmmm	47	orthorhombic	{3,4,3,4,4,4,4}	18	(7,8)
	sqc8365		Pmmm	47	orthorhombic	{4,3,4,4,4,4,4}	18	(7,8)
	sqc8771		Pmmm	47	orthorhombic	{4,4,4,8,4,4,4}	16	(7,8)
	sqc8963		Pmmm	47	orthorhombic	{4,4,8,4,4,4,4}	16	(7,8)
	sqc14533		Pmmm	47	orthorhombic	{8,3}	3	(2,4)
	sqc14534		Pmmm	47	orthorhombic	{6,4,3}	4	(3,4)
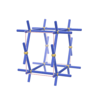
	sqc14535		Pmmm	47	orthorhombic	{6,3}	4	(2,5)
	sqc14537		Pmmm	47	orthorhombic	{8,3,4}	4	(3,5)
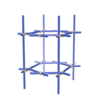
	sqc14538		Pmmm	47	orthorhombic	{4,4,3}	5	(3,5)
	sqc14539		Pmmm	47	orthorhombic	{12,3}	3	(2,5)
	sqc14540		Pmmm	47	orthorhombic	{4,6,3,4}	5	(4,5)
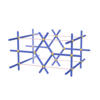
	sqc14541		Pmmm	47	orthorhombic	{4,4,3,3}	6	(4,5)
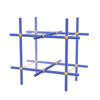
	sqc14643		Pmmm	47	orthorhombic	{5,5}	4	(2,5)
	sqc14542		Pmmm	47	orthorhombic	{8,5}	3	(2,5)
	sqc14543		Pmmm	47	orthorhombic	{3,8}	4	(2,6)
	sqc14545		Pmmm	47	orthorhombic	{8,3}	4	(2,6)
	sqc14546		Pmmm	47	orthorhombic	{5,6}	4	(2,6)
	sqc14547		Pmmm	47	orthorhombic	{3,4,4,4}	6	(4,6)