Pmmm

Number	47
Symmetry Class	orthorhombic
Chiral	N

s-nets

833 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
	sqc1475		Pmmm	47	orthorhombic	{3,4,4,4,4,8}	7	(6,7)
	sqc1476		Pmmm	47	orthorhombic	{4,3,4,4,8,4}	7	(6,7)
	sqc1477		Pmmm	47	orthorhombic	{3,4,4,4,8,4}	7	(6,7)
	sqc1479		Pmmm	47	orthorhombic	{7,4}	6	(2,7)
	sqc1482		Pmmm	47	orthorhombic	{4,7}	6	(2,7)
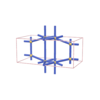
	sqc1483		Pmmm	47	orthorhombic	{4,7}	6	(2,7)
	sqc1484		Pmmm	47	orthorhombic	{4,7}	6	(2,7)
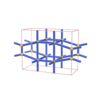
	sqc1486		Pmmm	47	orthorhombic	{6,3}	6	(2,6)
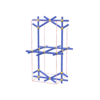
	sqc1489		Pmmm	47	orthorhombic	{3,6}	6	(2,6)
	sqc1490		Pmmm	47	orthorhombic	{4,6,4,4,4,4}	7	(6,7)
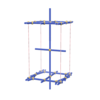
	sqc1491		Pmmm	47	orthorhombic	{4,4,4,4,6,4}	7	(6,7)
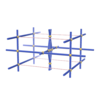
	sqc1492		Pmmm	47	orthorhombic	{4,4,4,6,4,4}	7	(6,7)
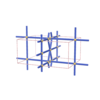
	sqc1493		Pmmm	47	orthorhombic	{4,6,4,4,4,4}	7	(6,7)
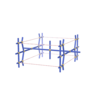
	sqc1494		Pmmm	47	orthorhombic	{4,6,4,4,4,4}	7	(6,7)
	sqc1495		Pmmm	47	orthorhombic	{3,4,4,4,4,4}	8	(6,7)
	sqc1496		Pmmm	47	orthorhombic	{3,4,4,4,4,4}	8	(6,7)
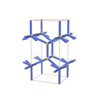
	sqc1499		Pmmm	47	orthorhombic	{4,7}	6	(2,5)
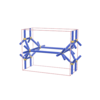
	sqc1500		Pmmm	47	orthorhombic	{7,4}	6	(2,5)
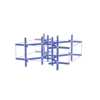
	sqc1501		Pmmm	47	orthorhombic	{4,7}	6	(2,5)
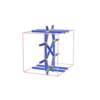
	sqc1511		Pmmm	47	orthorhombic	{5,5}	6	(2,6)
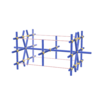
	sqc1513		Pmmm	47	orthorhombic	{5,5}	6	(2,7)
	sqc1517		Pmmm	47	orthorhombic	{3,4,4,4,8,4}	7	(6,7)
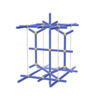
	sqc1518		Pmmm	47	orthorhombic	{4,8,4,3,4,4}	7	(6,7)
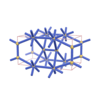
	sqc1520		Pmmm	47	orthorhombic	{3,7,5}	6	(3,5)
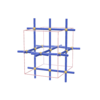
	sqc1524		Pmmm	47	orthorhombic	{4,4,6,4,4,4}	7	(6,7)
	sqc1529		Pmmm	47	orthorhombic	{6,6,3}	6	(3,5)
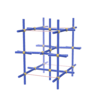
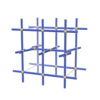
	sqc1530		Pmmm	47	orthorhombic	{4,6,4,4,4,4}	7	(6,7)
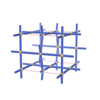
	sqc1531		Pmmm	47	orthorhombic	{4,4,6,4,4,4}	7	(6,7)
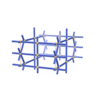
	sqc1532		Pmmm	47	orthorhombic	{4,4,4,4,4,6}	7	(6,7)
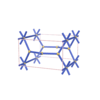
	sqc1533		Pmmm	47	orthorhombic	{4,4,4,4,4,6}	7	(6,7)
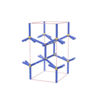
	sqc1534		Pmmm	47	orthorhombic	{6,3,3}	8	(3,5)
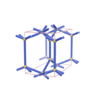
	sqc1540		Pmmm	47	orthorhombic	{5,5}	6	(2,5)
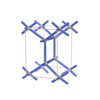
	sqc1541		Pmmm	47	orthorhombic	{5,7,3}	6	(3,5)
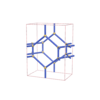
	sqc1542		Pmmm	47	orthorhombic	{5,5}	6	(2,5)
	sqc1544		Pmmm	47	orthorhombic	{4,4,3}	8	(3,4)
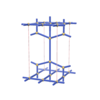
	sqc1545		Pmmm	47	orthorhombic	{3,4,4,8,4,4}	7	(6,7)
	sqc1547		Pmmm	47	orthorhombic	{4,4,3,4,4,4}	8	(6,7)
	sqc1550		Pmmm	47	orthorhombic	{5,5}	6	(2,5)
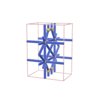
	sqc1553		Pmmm	47	orthorhombic	{6,3,3}	8	(3,5)
	sqc1608		Pmmm	47	orthorhombic	{3,10}	6	(2,8)
	sqc1609		Pmmm	47	orthorhombic	{3,10}	6	(2,8)
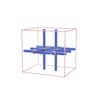
	sqc1610		Pmmm	47	orthorhombic	{3,10}	6	(2,8)
	sqc1673		Pmmm	47	orthorhombic	{4,8}	6	(2,8)
	sqc1680		Pmmm	47	orthorhombic	{8,4}	6	(2,6)
	sqc1689		Pmmm	47	orthorhombic	{4,8}	6	(2,6)
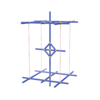
	sqc1695		Pmmm	47	orthorhombic	{8,4}	6	(2,6)
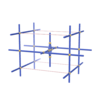
	sqc1702		Pmmm	47	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
	sqc1703		Pmmm	47	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
	sqc1704		Pmmm	47	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
	sqc1705		Pmmm	47	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
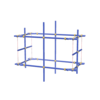
	sqc1706		Pmmm	47	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
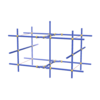
	sqc1707		Pmmm	47	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
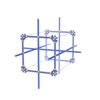
	sqc1708		Pmmm	47	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
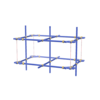
	sqc1709		Pmmm	47	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
	sqc1710		Pmmm	47	orthorhombic	{4,4,4,4,4,4}	8	(6,8)
	sqc1733		Pmmm	47	orthorhombic	{3,6,4,3}	8	(4,6)
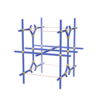
	sqc1848		Pmmm	47	orthorhombic	{4,4,4,8,8,4}	6	(6,7)
	sqc1896		Pmmm	47	orthorhombic	{3,3,4,4,4,4,4}	9	(7,7)
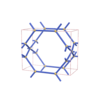
	sqc1985		Pmmm	47	orthorhombic	{3,4,5}	8	(3,5)
	sqc1986		Pmmm	47	orthorhombic	{3,4,5}	8	(3,5)
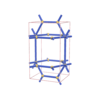
	sqc1987		Pmmm	47	orthorhombic	{5,4,3}	8	(3,5)
	sqc1995		Pmmm	47	orthorhombic	{3,7,3}	8	(3,5)
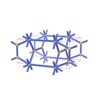
	sqc2002		Pmmm	47	orthorhombic	{3,7,3}	8	(3,5)
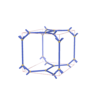
	sqc2158		Pmmm	47	orthorhombic	{5,4,3}	8	(3,5)
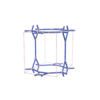
	sqc2194		Pmmm	47	orthorhombic	{3,3,4,3}	10	(4,6)
	sqc2213		Pmmm	47	orthorhombic	{4,9}	6	(2,8)
	sqc2214		Pmmm	47	orthorhombic	{4,9}	6	(2,8)
	sqc2221		Pmmm	47	orthorhombic	{7,3}	6	(2,7)
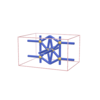
	sqc2223		Pmmm	47	orthorhombic	{5,7}	6	(2,8)
	sqc2228		Pmmm	47	orthorhombic	{4,4,3,4,4,4,4}	9	(7,8)
	sqc2229		Pmmm	47	orthorhombic	{4,4,4,3,4,4,4}	9	(7,8)
	sqc2232		Pmmm	47	orthorhombic	{5,6}	6	(2,5)
	sqc2233		Pmmm	47	orthorhombic	{7,5}	6	(2,6)
	sqc2239		Pmmm	47	orthorhombic	{5,7}	6	(2,6)
	sqc2258		Pmmm	47	orthorhombic	{4,4,4,4,4,3,4}	9	(7,8)
	sqc2259		Pmmm	47	orthorhombic	{4,4,4,4,3,4,4}	9	(7,8)
	sqc2260		Pmmm	47	orthorhombic	{3,4,4,4,4,4,4}	9	(7,8)
	sqc2261		Pmmm	47	orthorhombic	{3,4,4,4,4,4,4}	9	(7,8)
	sqc2264		Pmmm	47	orthorhombic	{6,4,3}	8	(3,6)
	sqc2266		Pmmm	47	orthorhombic	{4,6,3}	8	(3,5)
	sqc2267		Pmmm	47	orthorhombic	{5,6}	6	(2,6)
	sqc2269		Pmmm	47	orthorhombic	{3,4,3}	10	(3,5)
	sqc2270		Pmmm	47	orthorhombic	{3,4,4,4,4,4,4}	9	(7,8)
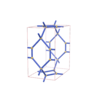
	sqc2284		Pmmm	47	orthorhombic	{4,3,3}	10	(3,5)
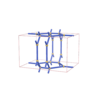
	sqc2285		Pmmm	47	orthorhombic	{3,4,4,3}	10	(4,6)
	sqc2286		Pmmm	47	orthorhombic	{3,4,3}	10	(3,5)
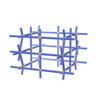
	sqc2403		Pmmm	47	orthorhombic	{3,6}	8	(2,7)
	sqc2602		Pmmm	47	orthorhombic	{4,4,4,4,8,4,4}	8	(7,8)
	sqc2731		Pmmm	47	orthorhombic	{4,4,4,8,4,4,4}	8	(7,8)
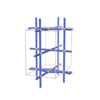
	sqc2732		Pmmm	47	orthorhombic	{4,8,4,4,4,4,4}	8	(7,8)
	sqc2733		Pmmm	47	orthorhombic	{4,4,8,4,4,4,4}	8	(7,8)
	sqc2748		Pmmm	47	orthorhombic	{3,6,3,3}	10	(4,5)
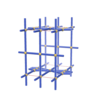
	sqc2751		Pmmm	47	orthorhombic	{5,3,4,3}	10	(4,5)
	sqc2803		Pmmm	47	orthorhombic	{4,4,4,4,4,8,4}	8	(7,8)
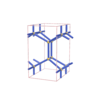
	sqc2836		Pmmm	47	orthorhombic	{4,7,3}	8	(3,6)
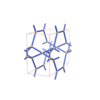
	sqc2841		Pmmm	47	orthorhombic	{5,4}	8	(2,6)
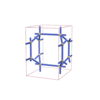
	sqc2843		Pmmm	47	orthorhombic	{3,4,4,3}	10	(4,5)
	sqc2920		Pmmm	47	orthorhombic	{4,5}	8	(2,6)
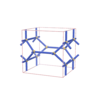
	sqc2926		Pmmm	47	orthorhombic	{5,4}	8	(2,6)
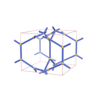
	sqc2994		Pmmm	47	orthorhombic	{3,3,6,3}	10	(4,5)