Cmma

Number	67
Symmetry Class	orthorhombic
Chiral	N

s-nets

872 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
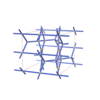
	sqc4650		Cmma	67	orthorhombic	{4,4,4,6}	10	(4,6)
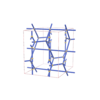
	sqc4651		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
	sqc4653		Cmma	67	orthorhombic	{4,4,4,3}	12	(4,6)
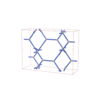
	sqc4656		Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
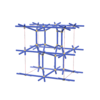
	sqc4663		Cmma	67	orthorhombic	{3,4}	12	(2,5)
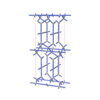
	sqc4667		Cmma	67	orthorhombic	{6,4}	10	(2,5)
	sqc4668		Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
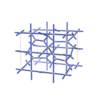
	sqc4669		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
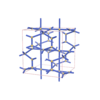
	sqc4672		Cmma	67	orthorhombic	{4,4,4,3}	12	(4,6)
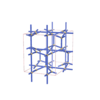
	sqc4673		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
	sqc4677		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
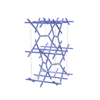
	sqc4686		Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
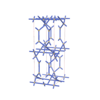
	sqc4691		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
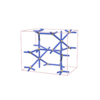
	sqc4696		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
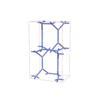
	sqc4699		Cmma	67	orthorhombic	{6,4}	10	(2,5)
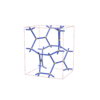
	sqc4702		Cmma	67	orthorhombic	{4,3}	12	(2,5)
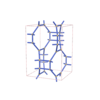
	sqc4706		Cmma	67	orthorhombic	{4,3}	12	(2,5)
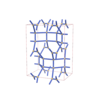
	sqc4707		Cmma	67	orthorhombic	{4,3}	12	(2,5)
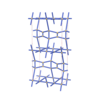
	sqc4712		Cmma	67	orthorhombic	{4,3}	12	(2,5)
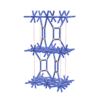
	sqc4715		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
	sqc4784		Cmma	67	orthorhombic	{12,3}	10	(2,6)
	sqc4785		Cmma	67	orthorhombic	{10,4}	6	(2,6)
	sqc4806		Cmma	67	orthorhombic	{8,8,4,4}	8	(4,6)
	sqc4835		Cmma	67	orthorhombic	{8,4}	8	(2,7)
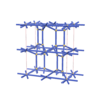
	sqc4841		Cmma	67	orthorhombic	{4,8}	10	(2,6)
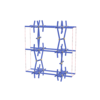
	sqc4845		Cmma	67	orthorhombic	{8,4}	10	(2,6)
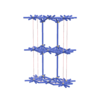
	sqc4847		Cmma	67	orthorhombic	{8,4}	8	(2,7)
	sqc4848		Cmma	67	orthorhombic	{10,7}	6	(2,6)
	sqc4849		Cmma	67	orthorhombic	{5,7}	8	(2,6)
	sqc4852		Cmma	67	orthorhombic	{4,4,8,4}	10	(4,6)
	sqc4861		Cmma	67	orthorhombic	{4,8,4,4}	10	(4,6)
	sqc4872		Cmma	67	orthorhombic	{6,6}	8	(2,7)
	sqc4876		Cmma	67	orthorhombic	{6,3}	12	(2,6)
	sqc4893		Cmma	67	orthorhombic	{4,4,4,3,3}	14	(5,6)
	sqc4898		Cmma	67	orthorhombic	{4,4,4,4}	12	(4,7)
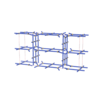
	sqc4899		Cmma	67	orthorhombic	{4,3,3,4,4}	14	(5,6)
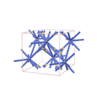
	sqc4910		Cmma	67	orthorhombic	{12,3}	10	(2,6)
	sqc4913		Cmma	67	orthorhombic	{3,12}	10	(2,6)
	sqc5022		Cmma	67	orthorhombic	{9,3}	8	(2,7)
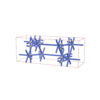
	sqc5023		Cmma	67	orthorhombic	{8,4}	8	(2,7)
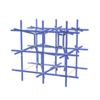
	sqc5025		Cmma	67	orthorhombic	{8,4}	10	(2,6)
	sqc5028		Cmma	67	orthorhombic	{4,8}	10	(2,6)
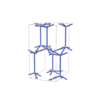
	sqc5045		Cmma	67	orthorhombic	{6,3}	12	(2,6)
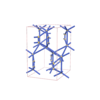
	sqc5048		Cmma	67	orthorhombic	{6,3}	12	(2,6)
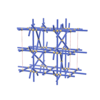
	sqc5063		Cmma	67	orthorhombic	{4,4,4,4,4}	12	(5,6)
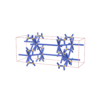
	sqc5074		Cmma	67	orthorhombic	{3,6}	12	(2,6)
	sqc5082		Cmma	67	orthorhombic	{3,9}	8	(2,7)
	sqc5083		Cmma	67	orthorhombic	{9,3}	8	(2,7)
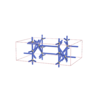
	sqc5084		Cmma	67	orthorhombic	{3,9}	8	(2,7)
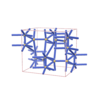
	sqc5086		Cmma	67	orthorhombic	{5,7}	8	(2,6)
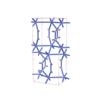
	sqc5094		Cmma	67	orthorhombic	{5,7}	8	(2,7)
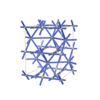
	sqc5102		Cmma	67	orthorhombic	{6,3}	12	(2,6)
	sqc5114		Cmma	67	orthorhombic	{4,8,4,4}	10	(4,6)
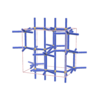
	sqc5130		Cmma	67	orthorhombic	{7,5}	8	(2,6)
	sqc5152		Cmma	67	orthorhombic	{7,5}	8	(2,7)
	sqc5155		Cmma	67	orthorhombic	{4,3,4,4,6}	12	(5,5)
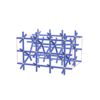
	sqc5161		Cmma	67	orthorhombic	{6,3}	12	(2,6)
	sqc5163		Cmma	67	orthorhombic	{6,6}	8	(2,7)
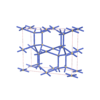
	sqc5171		Cmma	67	orthorhombic	{6,6}	8	(2,7)
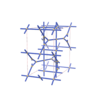
	sqc5203		Cmma	67	orthorhombic	{4,5}	10	(2,5)
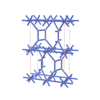
	sqc5208		Cmma	67	orthorhombic	{4,3,3,4,4}	14	(5,6)
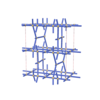
	sqc5266		Cmma	67	orthorhombic	{8,4}	10	(2,6)
	sqc5271		Cmma	67	orthorhombic	{4,4,4,4}	12	(4,7)
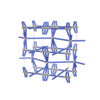
	sqc5297		Cmma	67	orthorhombic	{4,4,8,4}	10	(4,6)
	sqc5311		Cmma	67	orthorhombic	{4,4,8,4}	10	(4,6)
	sqc5312		Cmma	67	orthorhombic	{4,8,4,4}	10	(4,6)
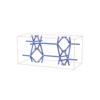
	sqc5314		Cmma	67	orthorhombic	{3,6}	12	(2,6)
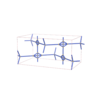
	sqc5315		Cmma	67	orthorhombic	{3,6}	12	(2,6)
	sqc5316		Cmma	67	orthorhombic	{4,4,4,4}	12	(4,6)
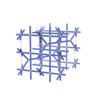
	sqc5329		Cmma	67	orthorhombic	{3,6}	12	(2,6)
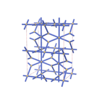
	sqc5336		Cmma	67	orthorhombic	{4,6,3,4,4}	12	(5,6)
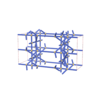
	sqc5340		Cmma	67	orthorhombic	{6,3,4,4,4}	12	(5,5)
	sqc5348		Cmma	67	orthorhombic	{4,8,4,4}	10	(4,6)
	sqc5357		Cmma	67	orthorhombic	{4,8,4,4}	10	(4,6)
	sqc5378		Cmma	67	orthorhombic	{4,6,3,4,4}	12	(5,6)
	sqc5380		Cmma	67	orthorhombic	{3,4,4,4,6}	12	(5,5)
	sqc5382		Cmma	67	orthorhombic	{4,4,8,4}	10	(4,6)
	sqc5389		Cmma	67	orthorhombic	{4,8,4,4}	10	(4,6)
	sqc5392		Cmma	67	orthorhombic	{4,4,4,8}	10	(4,6)
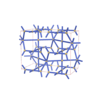
	sqc5406		Cmma	67	orthorhombic	{4,8,4,4}	10	(4,6)
	sqc5408		Cmma	67	orthorhombic	{4,4,4,8}	10	(4,6)
	sqc5434		Cmma	67	orthorhombic	{3,4,4,4,6}	12	(5,5)
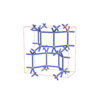
	sqc5436		Cmma	67	orthorhombic	{4,3,4,6,4}	12	(5,5)
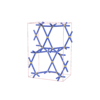
	sqc5445		Cmma	67	orthorhombic	{5,4}	10	(2,5)
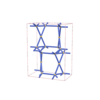
	sqc5458		Cmma	67	orthorhombic	{5,4}	10	(2,5)
	sqc5460		Cmma	67	orthorhombic	{5,4}	10	(2,5)
	sqc5463		Cmma	67	orthorhombic	{5,4}	10	(2,5)
	sqc5465		Cmma	67	orthorhombic	{5,4}	10	(2,5)
	sqc5495		Cmma	67	orthorhombic	{4,4,4,4}	12	(4,6)
	sqc5506		Cmma	67	orthorhombic	{4,4,3,3,4}	14	(5,6)
	sqc5511		Cmma	67	orthorhombic	{4,4}	12	(2,6)
	sqc5517		Cmma	67	orthorhombic	{4,4,4,4}	12	(4,7)
	sqc5519		Cmma	67	orthorhombic	{4,4,4,4}	12	(4,6)
	sqc5534		Cmma	67	orthorhombic	{4,4}	12	(2,6)
	sqc5538		Cmma	67	orthorhombic	{4,4,4,4}	12	(4,7)
	sqc5552		Cmma	67	orthorhombic	{4,4}	12	(2,6)
	sqc5563		Cmma	67	orthorhombic	{4,4,4,4,4}	12	(5,6)
	sqc5566		Cmma	67	orthorhombic	{4,4}	12	(2,6)
	sqc5573		Cmma	67	orthorhombic	{4,4}	12	(2,6)
	sqc5581		Cmma	67	orthorhombic	{4,4}	12	(2,6)