Cmma

Number	67
Symmetry Class	orthorhombic
Chiral	N

s-nets

872 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
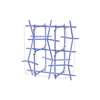
	sqc7370		Cmma	67	orthorhombic	{3,4,4,4,4,4}	16	(6,7)
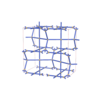
	sqc7371		Cmma	67	orthorhombic	{4,4,4,4,3,4}	16	(6,7)
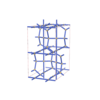
	sqc7372		Cmma	67	orthorhombic	{4,3,4,4,4,4}	16	(6,7)
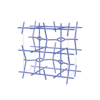
	sqc7374		Cmma	67	orthorhombic	{4,3,4,4,4,4}	16	(6,7)
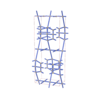
	sqc7382		Cmma	67	orthorhombic	{4,4,4,4,3,4}	16	(6,7)
	sqc7383		Cmma	67	orthorhombic	{3,4,4,4,4,4}	16	(6,7)
	sqc7420		Cmma	67	orthorhombic	{10,3}	12	(2,8)
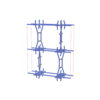
	sqc7437		Cmma	67	orthorhombic	{8,4}	12	(2,8)
	sqc7439		Cmma	67	orthorhombic	{8,4}	12	(2,8)
	sqc7447		Cmma	67	orthorhombic	{6,5}	12	(2,8)
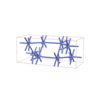
	sqc7458		Cmma	67	orthorhombic	{4,4,4,4,4,4}	16	(6,8)
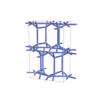
	sqc7553		Cmma	67	orthorhombic	{8,4}	12	(2,8)
	sqc7592		Cmma	67	orthorhombic	{6,5}	12	(2,8)
	sqc7609		Cmma	67	orthorhombic	{4,7}	10	(2,7)
	sqc7627		Cmma	67	orthorhombic	{4,4,4,4,4,8}	14	(6,7)
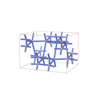
	sqc7648		Cmma	67	orthorhombic	{6,5}	12	(2,8)
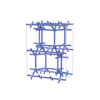
	sqc7658		Cmma	67	orthorhombic	{4,6}	12	(2,8)
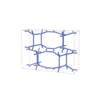
	sqc7687		Cmma	67	orthorhombic	{3,5}	16	(2,7)
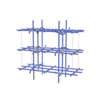
	sqc7851		Cmma	67	orthorhombic	{4,4,4,4,4,4}	16	(6,8)
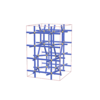
	sqc7891		Cmma	67	orthorhombic	{6,5}	12	(2,8)
	sqc7904		Cmma	67	orthorhombic	{4,4,4,4,4,8}	14	(6,7)
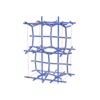
	sqc7909		Cmma	67	orthorhombic	{4,4,4,4,4,8}	14	(6,7)
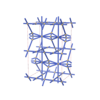
	sqc7913		Cmma	67	orthorhombic	{4,4,4,4,4,8}	14	(6,7)
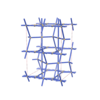
	sqc7915		Cmma	67	orthorhombic	{4,4,4,4,4,8}	14	(6,7)
	sqc7917		Cmma	67	orthorhombic	{4,4,4,4,4,8}	14	(6,7)
	sqc7932		Cmma	67	orthorhombic	{4,4,8,4,4,4}	14	(6,7)
	sqc7998		Cmma	67	orthorhombic	{5,3}	16	(2,7)
	sqc8002		Cmma	67	orthorhombic	{3,5}	16	(2,7)
	sqc8012		Cmma	67	orthorhombic	{3,5}	16	(2,7)
	sqc8014		Cmma	67	orthorhombic	{5,3}	16	(2,7)
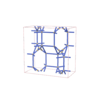
	sqc8023		Cmma	67	orthorhombic	{3,5}	16	(2,7)
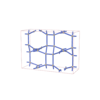
	sqc8064		Cmma	67	orthorhombic	{4,4}	16	(2,7)
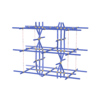
	sqc8069		Cmma	67	orthorhombic	{4,4,4,4,4,4}	16	(6,8)
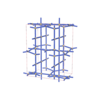
	sqc8071		Cmma	67	orthorhombic	{4,4,4,4,4,4}	16	(6,8)
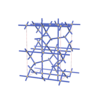
	sqc8075		Cmma	67	orthorhombic	{4,4,4,4,4,4}	16	(6,8)
	sqc8097		Cmma	67	orthorhombic	{4,4,4,4,4,4}	16	(6,8)
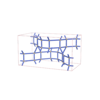
	sqc8114		Cmma	67	orthorhombic	{4,4}	16	(2,7)
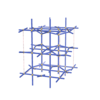
	sqc8136		Cmma	67	orthorhombic	{4,4,4,4,4,4}	16	(6,8)
	sqc8271		Cmma	67	orthorhombic	{7,5}	12	(2,8)
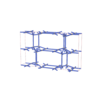
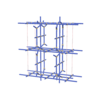
	sqc8276		Cmma	67	orthorhombic	{5,6}	12	(2,8)
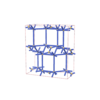
	sqc8283		Cmma	67	orthorhombic	{4,4,4,3,4,4,4}	18	(7,8)
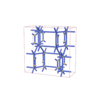
	sqc8290		Cmma	67	orthorhombic	{3,7}	12	(2,8)
	sqc8291		Cmma	67	orthorhombic	{3,7}	12	(2,8)
	sqc8298		Cmma	67	orthorhombic	{3,7}	12	(2,8)
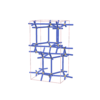
	sqc8301		Cmma	67	orthorhombic	{5,6}	12	(2,8)
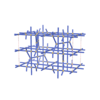
	sqc8303		Cmma	67	orthorhombic	{5,6}	12	(2,8)
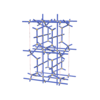
	sqc8330		Cmma	67	orthorhombic	{4,4,3,4,4,4,4}	18	(7,8)
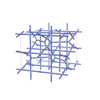
	sqc8382		Cmma	67	orthorhombic	{4,4,3,4,4,4,4}	18	(7,8)
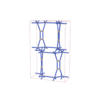
	sqc8385		Cmma	67	orthorhombic	{4,4,4,3,4,4,4}	18	(7,8)
	sqc8627		Cmma	67	orthorhombic	{3,6}	16	(2,8)
	sqc8705		Cmma	67	orthorhombic	{3,6}	16	(2,8)
	sqc8713		Cmma	67	orthorhombic	{3,6}	16	(2,8)
	sqc8736		Cmma	67	orthorhombic	{4,5}	16	(2,8)
	sqc8743		Cmma	67	orthorhombic	{4,5}	16	(2,8)
	sqc8935		Cmma	67	orthorhombic	{4,4,4,8,4,4,4}	16	(7,8)
	sqc8939		Cmma	67	orthorhombic	{4,4,4,8,4,4,4}	16	(7,8)
	sqc9021		Cmma	67	orthorhombic	{3,6}	16	(2,8)
	sqc9022		Cmma	67	orthorhombic	{6,3}	16	(2,8)
	sqc9088		Cmma	67	orthorhombic	{5,4}	16	(2,8)
	sqc9094		Cmma	67	orthorhombic	{4,5}	16	(2,8)
	sqc9110		Cmma	67	orthorhombic	{4,5}	16	(2,8)
	sqc9178		Cmma	67	orthorhombic	{4,4,4,4,4,4,4}	18	(7,8)
	sqc9179		Cmma	67	orthorhombic	{4,4,4,4,4,4,4}	18	(7,8)
	sqc9204		Cmma	67	orthorhombic	{4,4,4,4,4,4,4}	18	(7,8)
	sqc9206		Cmma	67	orthorhombic	{4,4,4,4,4,4,4}	18	(7,8)
	sqc9481		Cmma	67	orthorhombic	{3,7}	16	(2,9)
	sqc9535		Cmma	67	orthorhombic	{4,6}	16	(2,9)
	sqc9898		Cmma	67	orthorhombic	{4,4,4,4,4,4,4,4}	20	(8,9)
	sqc14614		Cmma	67	orthorhombic	{3,6,4}	8	(3,4)
	sqc14617		Cmma	67	orthorhombic	{4,8,3}	8	(3,5)
	sqc14620		Cmma	67	orthorhombic	{3,3,4,4}	12	(4,5)
	sqc14623		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)