Cmma

Number	67
Symmetry Class	orthorhombic
Chiral	N

s-nets

872 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
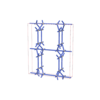
	sqc4135		Cmma	67	orthorhombic	{4,8,3,4}	10	(4,6)
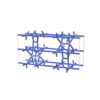
	sqc4141		Cmma	67	orthorhombic	{5,6}	8	(2,6)
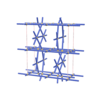
	sqc4142		Cmma	67	orthorhombic	{6,5}	8	(2,6)
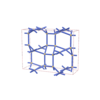
	sqc4150		Cmma	67	orthorhombic	{4,4,4,6}	10	(4,6)
	sqc4151		Cmma	67	orthorhombic	{6,4}	10	(2,5)
	sqc4158		Cmma	67	orthorhombic	{6,4,4,4}	10	(4,6)
	sqc4159		Cmma	67	orthorhombic	{5,12}	6	(2,6)
	sqc4164		Cmma	67	orthorhombic	{6,5}	8	(2,6)
	sqc4166		Cmma	67	orthorhombic	{5,6}	8	(2,6)
	sqc4178		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
	sqc4180		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
	sqc4181		Cmma	67	orthorhombic	{6,4,4,4}	10	(4,6)
	sqc4187		Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
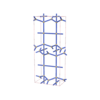
	sqc4191		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
	sqc4192		Cmma	67	orthorhombic	{4,4,4,3}	12	(4,6)
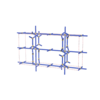
	sqc4193		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
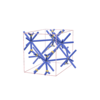
	sqc4194		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
	sqc4200		Cmma	67	orthorhombic	{3,10}	10	(2,5)
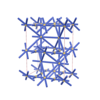
	sqc4256		Cmma	67	orthorhombic	{4,4,6,8}	8	(4,5)
	sqc4257		Cmma	67	orthorhombic	{4,4,8,6}	8	(4,5)
	sqc4258		Cmma	67	orthorhombic	{3,10}	10	(2,5)
	sqc4259		Cmma	67	orthorhombic	{9,4}	6	(2,6)
	sqc4262		Cmma	67	orthorhombic	{6,8}	6	(2,6)
	sqc4263		Cmma	67	orthorhombic	{3,8}	8	(2,6)
	sqc4264		Cmma	67	orthorhombic	{3,8}	8	(2,6)
	sqc4265		Cmma	67	orthorhombic	{4,7}	8	(2,7)
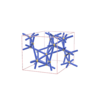
	sqc4276		Cmma	67	orthorhombic	{6,5}	8	(2,6)
	sqc4280		Cmma	67	orthorhombic	{6,5}	8	(2,6)
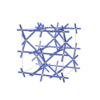
	sqc4286		Cmma	67	orthorhombic	{4,8,6,4}	8	(4,5)
	sqc4291		Cmma	67	orthorhombic	{4,6,4,4}	10	(4,5)
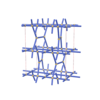
	sqc4297		Cmma	67	orthorhombic	{4,4,4,3}	12	(4,6)
	sqc4298		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
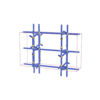
	sqc4301		Cmma	67	orthorhombic	{8,6,4,4}	8	(4,5)
	sqc4306		Cmma	67	orthorhombic	{8,3}	8	(2,6)
	sqc4307		Cmma	67	orthorhombic	{3,8}	8	(2,6)
	sqc4313		Cmma	67	orthorhombic	{5,6}	8	(2,6)
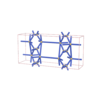
	sqc4315		Cmma	67	orthorhombic	{6,5}	8	(2,6)
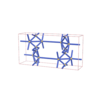
	sqc4318		Cmma	67	orthorhombic	{6,5}	8	(2,6)
	sqc4320		Cmma	67	orthorhombic	{6,5}	8	(2,6)
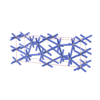
	sqc4326		Cmma	67	orthorhombic	{9,4}	6	(2,6)
	sqc4327		Cmma	67	orthorhombic	{6,8}	6	(2,6)
	sqc4328		Cmma	67	orthorhombic	{3,8}	8	(2,6)
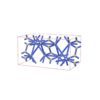
	sqc4329		Cmma	67	orthorhombic	{3,8}	8	(2,6)
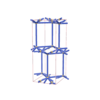
	sqc4330		Cmma	67	orthorhombic	{3,8}	8	(2,6)
	sqc4331		Cmma	67	orthorhombic	{3,8}	8	(2,6)
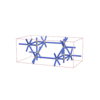
	sqc4332		Cmma	67	orthorhombic	{3,8}	8	(2,6)
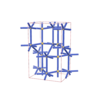
	sqc4334		Cmma	67	orthorhombic	{7,4}	8	(2,6)
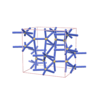
	sqc4347		Cmma	67	orthorhombic	{7,4}	8	(2,7)
	sqc4350		Cmma	67	orthorhombic	{5,6}	8	(2,6)
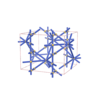
	sqc4353		Cmma	67	orthorhombic	{8,4,3,4}	10	(4,5)
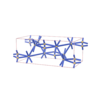
	sqc4357		Cmma	67	orthorhombic	{4,7}	8	(2,6)
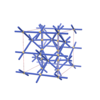
	sqc4370		Cmma	67	orthorhombic	{4,6,8,4}	8	(4,5)
	sqc4378		Cmma	67	orthorhombic	{8,3}	8	(2,6)
	sqc4379		Cmma	67	orthorhombic	{3,8}	8	(2,6)
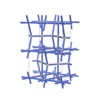
	sqc4380		Cmma	67	orthorhombic	{3,8}	8	(2,6)
	sqc4384		Cmma	67	orthorhombic	{8,4,4,6}	8	(4,5)
	sqc4389		Cmma	67	orthorhombic	{5,6}	8	(2,6)
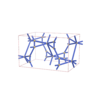
	sqc4394		Cmma	67	orthorhombic	{5,6}	8	(2,6)
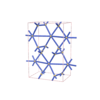
	sqc4403		Cmma	67	orthorhombic	{4,6}	10	(2,5)
	sqc4408		Cmma	67	orthorhombic	{4,6}	10	(2,5)
	sqc4409		Cmma	67	orthorhombic	{5,6}	8	(2,6)
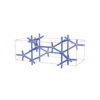
	sqc4412		Cmma	67	orthorhombic	{5,6}	8	(2,6)
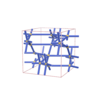
	sqc4414		Cmma	67	orthorhombic	{5,6}	8	(2,6)
	sqc4416		Cmma	67	orthorhombic	{5,6}	8	(2,6)
	sqc4417		Cmma	67	orthorhombic	{3,5}	12	(2,5)
	sqc4419		Cmma	67	orthorhombic	{3,5}	12	(2,5)
	sqc4420		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
	sqc4483		Cmma	67	orthorhombic	{6,4}	10	(2,5)
	sqc4517		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
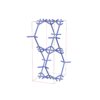
	sqc4519		Cmma	67	orthorhombic	{4,4,6,4}	10	(4,5)
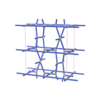
	sqc4522		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
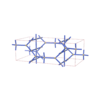
	sqc4524		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
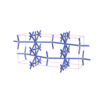
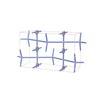
	sqc4535		Cmma	67	orthorhombic	{8,6,4,4}	8	(4,5)
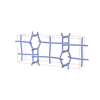
	sqc4536		Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
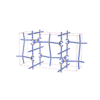
	sqc4537		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
	sqc4538		Cmma	67	orthorhombic	{4,4,4,3}	12	(4,6)
	sqc4539		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
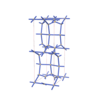
	sqc4541		Cmma	67	orthorhombic	{4,4,4,3}	12	(4,6)
	sqc4542		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
	sqc4551		Cmma	67	orthorhombic	{4,8,4,6}	8	(4,5)
	sqc4564		Cmma	67	orthorhombic	{4,4,6,4}	10	(4,6)
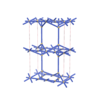
	sqc4566		Cmma	67	orthorhombic	{6,4,4,4}	10	(4,5)
	sqc4567		Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
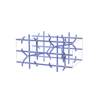
	sqc4568		Cmma	67	orthorhombic	{4,4,3,4}	12	(4,6)
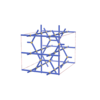
	sqc4571		Cmma	67	orthorhombic	{3,4,4,4}	12	(4,6)
	sqc4574		Cmma	67	orthorhombic	{4,8,3,4}	10	(4,6)
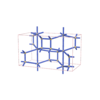
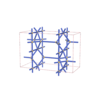
	sqc4588		Cmma	67	orthorhombic	{4,6}	10	(2,5)
	sqc4590		Cmma	67	orthorhombic	{4,4,4,6}	10	(4,5)
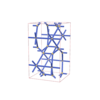
	sqc4591		Cmma	67	orthorhombic	{4,4,6,4}	10	(4,6)
	sqc4594		Cmma	67	orthorhombic	{4,6}	10	(2,5)
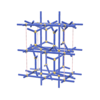
	sqc4597		Cmma	67	orthorhombic	{4,3,4,8}	10	(4,5)
	sqc4598		Cmma	67	orthorhombic	{3,8,4,4}	10	(4,6)
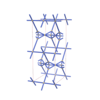
	sqc4599		Cmma	67	orthorhombic	{3,8,4,4}	10	(4,6)
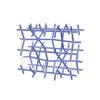
	sqc4606		Cmma	67	orthorhombic	{4,4,6,4}	10	(4,5)
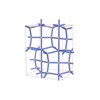
	sqc4608		Cmma	67	orthorhombic	{4,4,6,4}	10	(4,5)
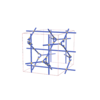
	sqc4609		Cmma	67	orthorhombic	{4,4,4,6}	10	(4,5)
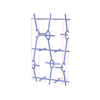
	sqc4639		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
	sqc4642		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
	sqc4645		Cmma	67	orthorhombic	{4,3,4,4}	12	(4,6)
	sqc4647		Cmma	67	orthorhombic	{4,6}	10	(2,5)