Cmma

Number	67
Symmetry Class	orthorhombic
Chiral	N

s-nets

872 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
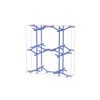
	sqc6313		Cmma	67	orthorhombic	{6,4}	12	(2,7)
	sqc6414		Cmma	67	orthorhombic	{8,4,4,4,8}	10	(5,6)
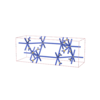
	sqc6422		Cmma	67	orthorhombic	{8,3}	12	(2,7)
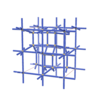
	sqc6423		Cmma	67	orthorhombic	{8,5}	10	(2,7)
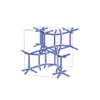
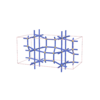
	sqc6440		Cmma	67	orthorhombic	{6,4}	12	(2,7)
	sqc6450		Cmma	67	orthorhombic	{4,6}	12	(2,7)
	sqc6467		Cmma	67	orthorhombic	{3,8}	12	(2,7)
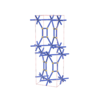
	sqc6469		Cmma	67	orthorhombic	{4,6}	12	(2,7)
	sqc6475		Cmma	67	orthorhombic	{8,3}	12	(2,7)
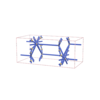
	sqc6476		Cmma	67	orthorhombic	{8,3}	12	(2,7)
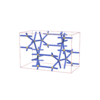
	sqc6477		Cmma	67	orthorhombic	{3,8}	12	(2,7)
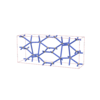
	sqc6485		Cmma	67	orthorhombic	{6,4}	12	(2,7)
	sqc6486		Cmma	67	orthorhombic	{6,4}	12	(2,7)
	sqc6509		Cmma	67	orthorhombic	{4,6}	10	(2,6)
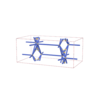
	sqc6522		Cmma	67	orthorhombic	{4,8,4,4,8}	10	(5,6)
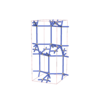
	sqc6527		Cmma	67	orthorhombic	{8,3}	12	(2,7)
	sqc6538		Cmma	67	orthorhombic	{6,4}	12	(2,7)
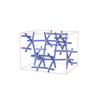
	sqc6542		Cmma	67	orthorhombic	{4,6}	10	(2,6)
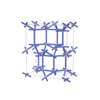
	sqc6544		Cmma	67	orthorhombic	{6,4}	12	(2,7)
	sqc6556		Cmma	67	orthorhombic	{4,6}	10	(2,6)
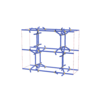
	sqc6580		Cmma	67	orthorhombic	{8,5}	10	(2,7)
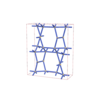
	sqc6581		Cmma	67	orthorhombic	{4,5}	12	(2,7)
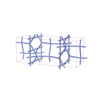
	sqc6590		Cmma	67	orthorhombic	{4,5}	12	(2,7)
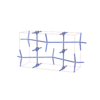
	sqc6652		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc6668		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc6669		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc6671		Cmma	67	orthorhombic	{4,6}	12	(2,7)
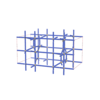
	sqc6686		Cmma	67	orthorhombic	{6,4}	12	(2,7)
	sqc6689		Cmma	67	orthorhombic	{6,4}	12	(2,7)
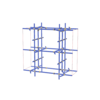
	sqc6707		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc6708		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
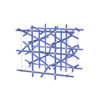
	sqc6716		Cmma	67	orthorhombic	{4,4,8,4,4}	12	(5,7)
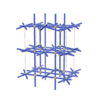
	sqc6724		Cmma	67	orthorhombic	{4,8,4,4,4}	12	(5,7)
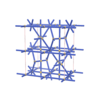
	sqc6760		Cmma	67	orthorhombic	{4,8,4,4,4}	12	(5,7)
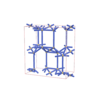
	sqc6763		Cmma	67	orthorhombic	{4,8,4,4,4}	12	(5,7)
	sqc6782		Cmma	67	orthorhombic	{6,4}	10	(2,6)
	sqc6783		Cmma	67	orthorhombic	{6,4}	10	(2,6)
	sqc6821		Cmma	67	orthorhombic	{4,5}	12	(2,7)
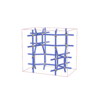
	sqc6828		Cmma	67	orthorhombic	{5,4}	12	(2,7)
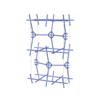
	sqc6831		Cmma	67	orthorhombic	{4,5}	12	(2,7)
	sqc6852		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
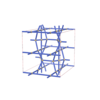
	sqc6861		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
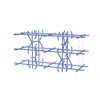
	sqc6872		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc6875		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc6901		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
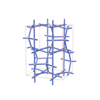
	sqc6902		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc6909		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc6911		Cmma	67	orthorhombic	{4,3}	16	(2,6)
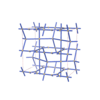
	sqc6913		Cmma	67	orthorhombic	{4,4,4,3,3,4}	16	(6,6)
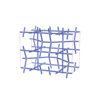
	sqc6914		Cmma	67	orthorhombic	{4,3,3,4,4,4}	16	(6,6)
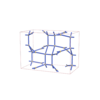
	sqc6933		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc6935		Cmma	67	orthorhombic	{4,3}	16	(2,6)
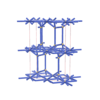
	sqc6936		Cmma	67	orthorhombic	{4,4,4,4,4}	14	(5,7)
	sqc7008		Cmma	67	orthorhombic	{10,5}	10	(2,7)
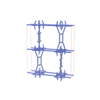
	sqc7026		Cmma	67	orthorhombic	{7,4}	12	(2,7)
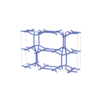
	sqc7034		Cmma	67	orthorhombic	{5,5}	12	(2,7)
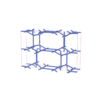
	sqc7036		Cmma	67	orthorhombic	{5,5}	12	(2,7)
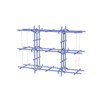
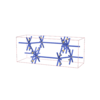
	sqc7041		Cmma	67	orthorhombic	{4,4,3,4,4,4}	16	(6,7)
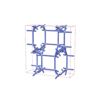
	sqc7075		Cmma	67	orthorhombic	{9,3}	12	(2,8)
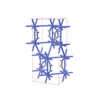
	sqc7090		Cmma	67	orthorhombic	{5,5}	12	(2,7)
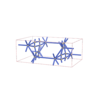
	sqc7091		Cmma	67	orthorhombic	{9,3}	12	(2,8)
	sqc7093		Cmma	67	orthorhombic	{4,7}	12	(2,7)
	sqc7095		Cmma	67	orthorhombic	{7,4}	12	(2,8)
	sqc7096		Cmma	67	orthorhombic	{4,7}	12	(2,7)
	sqc7099		Cmma	67	orthorhombic	{6,6}	10	(2,7)
	sqc7100		Cmma	67	orthorhombic	{3,6}	12	(2,7)
	sqc7101		Cmma	67	orthorhombic	{3,6}	12	(2,7)
	sqc7121		Cmma	67	orthorhombic	{6,6}	10	(2,7)
	sqc7122		Cmma	67	orthorhombic	{3,6}	12	(2,7)
	sqc7128		Cmma	67	orthorhombic	{3,6}	12	(2,7)
	sqc7129		Cmma	67	orthorhombic	{6,6}	10	(2,7)
	sqc7135		Cmma	67	orthorhombic	{3,6}	12	(2,7)
	sqc7136		Cmma	67	orthorhombic	{3,6}	12	(2,7)
	sqc7144		Cmma	67	orthorhombic	{5,5}	12	(2,7)
	sqc7145		Cmma	67	orthorhombic	{5,5}	12	(2,7)
	sqc7146		Cmma	67	orthorhombic	{5,5}	12	(2,7)
	sqc7152		Cmma	67	orthorhombic	{5,5}	12	(2,7)
	sqc7196		Cmma	67	orthorhombic	{3,4,4,4,4,4}	16	(6,7)
	sqc7211		Cmma	67	orthorhombic	{5,5}	12	(2,7)
	sqc7214		Cmma	67	orthorhombic	{5,5}	12	(2,7)
	sqc7215		Cmma	67	orthorhombic	{5,5}	12	(2,7)
	sqc7218		Cmma	67	orthorhombic	{4,3,4,4,4,4}	16	(6,7)
	sqc7219		Cmma	67	orthorhombic	{4,4,6,4,4,4}	14	(6,7)
	sqc7220		Cmma	67	orthorhombic	{4,3,4,4,4,4}	16	(6,7)
	sqc7240		Cmma	67	orthorhombic	{4,4,4,6,4,4}	14	(6,7)
	sqc7241		Cmma	67	orthorhombic	{4,4,6,4,4,4}	14	(6,7)
	sqc7248		Cmma	67	orthorhombic	{4,8,3,4,4,4}	14	(6,7)
	sqc7253		Cmma	67	orthorhombic	{4,8,3,4,4,4}	14	(6,7)
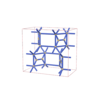
	sqc7285		Cmma	67	orthorhombic	{6,3}	12	(2,7)
	sqc7286		Cmma	67	orthorhombic	{6,3}	12	(2,7)
	sqc7287		Cmma	67	orthorhombic	{6,3}	12	(2,7)
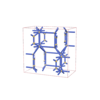
	sqc7288		Cmma	67	orthorhombic	{6,3}	12	(2,7)
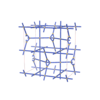
	sqc7289		Cmma	67	orthorhombic	{6,3}	12	(2,7)
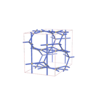
	sqc7334		Cmma	67	orthorhombic	{4,4,3,4,4,4}	16	(6,7)
	sqc7342		Cmma	67	orthorhombic	{3,4,4,4,4,4}	16	(6,7)
	sqc7347		Cmma	67	orthorhombic	{4,3,4,4,4,4}	16	(6,7)
	sqc7355		Cmma	67	orthorhombic	{4,4,3,4,4,4}	16	(6,7)
	sqc7364		Cmma	67	orthorhombic	{3,4,4,4,4,4}	16	(6,7)
	sqc7366		Cmma	67	orthorhombic	{4,4,4,6,4,4}	14	(6,7)
	sqc7369		Cmma	67	orthorhombic	{3,4,4,4,4,4}	16	(6,7)