Cmma

Number	67
Symmetry Class	orthorhombic
Chiral	N

s-nets

872 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
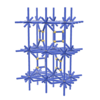
	sqc5583		Cmma	67	orthorhombic	{4,4,4,4}	12	(4,6)
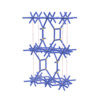
	sqc5639		Cmma	67	orthorhombic	{14,3}	10	(2,7)
	sqc5641		Cmma	67	orthorhombic	{10,4}	10	(2,6)
	sqc5642		Cmma	67	orthorhombic	{3,10}	8	(2,7)
	sqc5643		Cmma	67	orthorhombic	{10,3}	8	(2,7)
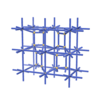
	sqc5649		Cmma	67	orthorhombic	{3,8,4,4,4}	12	(5,6)
	sqc5653		Cmma	67	orthorhombic	{10,4}	10	(2,7)
	sqc5679		Cmma	67	orthorhombic	{5,8}	8	(2,7)
	sqc5680		Cmma	67	orthorhombic	{7,6}	8	(2,7)
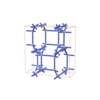
	sqc5685		Cmma	67	orthorhombic	{8,3,4,4,4}	12	(5,6)
	sqc5690		Cmma	67	orthorhombic	{5,6}	10	(2,6)
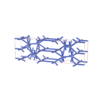
	sqc5698		Cmma	67	orthorhombic	{5,4}	12	(2,6)
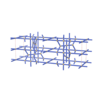
	sqc5703		Cmma	67	orthorhombic	{5,8}	8	(2,7)
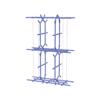
	sqc5707		Cmma	67	orthorhombic	{4,4,3,4,4}	14	(5,7)
	sqc5708		Cmma	67	orthorhombic	{4,4,4,3,4}	14	(5,7)
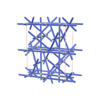
	sqc5715		Cmma	67	orthorhombic	{4,10}	10	(2,6)
	sqc5743		Cmma	67	orthorhombic	{4,8,6,4,4}	10	(5,6)
	sqc5748		Cmma	67	orthorhombic	{4,8,6,4,4}	10	(5,6)
	sqc5750		Cmma	67	orthorhombic	{4,10}	10	(2,6)
	sqc5752		Cmma	67	orthorhombic	{5,8}	8	(2,7)
	sqc5757		Cmma	67	orthorhombic	{4,4,6,4,4}	12	(5,6)
	sqc5760		Cmma	67	orthorhombic	{3,4,4,4,4}	14	(5,7)
	sqc5761		Cmma	67	orthorhombic	{3,4,4,4,4}	14	(5,7)
	sqc5764		Cmma	67	orthorhombic	{3,4,8,4,4}	12	(5,6)
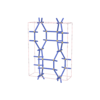
	sqc5777		Cmma	67	orthorhombic	{5,4}	12	(2,6)
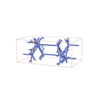
	sqc5779		Cmma	67	orthorhombic	{3,7}	12	(2,6)
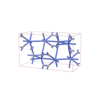
	sqc5784		Cmma	67	orthorhombic	{7,3}	12	(2,7)
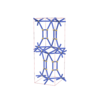
	sqc5788		Cmma	67	orthorhombic	{3,7}	12	(2,6)
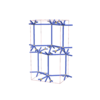
	sqc5807		Cmma	67	orthorhombic	{7,3}	12	(2,7)
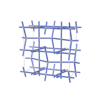
	sqc5811		Cmma	67	orthorhombic	{4,4,4,4,6}	12	(5,6)
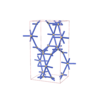
	sqc5818		Cmma	67	orthorhombic	{5,6}	10	(2,6)
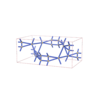
	sqc5826		Cmma	67	orthorhombic	{5,8}	8	(2,7)
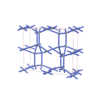
	sqc5829		Cmma	67	orthorhombic	{4,5}	12	(2,6)
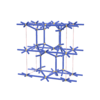
	sqc5831		Cmma	67	orthorhombic	{6,5}	10	(2,6)
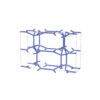
	sqc5832		Cmma	67	orthorhombic	{6,5}	10	(2,6)
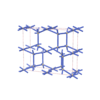
	sqc5833		Cmma	67	orthorhombic	{3,5}	12	(2,6)
	sqc5837		Cmma	67	orthorhombic	{6,5}	10	(2,6)
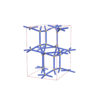
	sqc5845		Cmma	67	orthorhombic	{4,5}	12	(2,6)
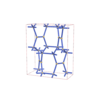
	sqc5848		Cmma	67	orthorhombic	{3,5}	12	(2,6)
	sqc5850		Cmma	67	orthorhombic	{4,5}	12	(2,6)
	sqc5851		Cmma	67	orthorhombic	{5,4}	12	(2,6)
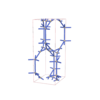
	sqc5853		Cmma	67	orthorhombic	{5,4}	12	(2,6)
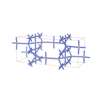
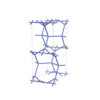
	sqc5907		Cmma	67	orthorhombic	{6,4,4,4,4}	12	(5,6)
	sqc5909		Cmma	67	orthorhombic	{4,3,4,4,4}	14	(5,6)
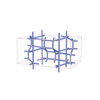
	sqc5925		Cmma	67	orthorhombic	{4,4,4,6,4}	12	(5,6)
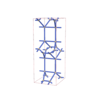
	sqc5942		Cmma	67	orthorhombic	{5,4}	12	(2,6)
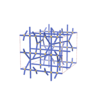
	sqc5946		Cmma	67	orthorhombic	{4,5}	12	(2,6)
	sqc5947		Cmma	67	orthorhombic	{4,4,6,4,4}	12	(5,6)
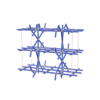
	sqc5948		Cmma	67	orthorhombic	{4,4,3,4,4}	14	(5,7)
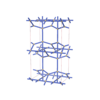
	sqc5949		Cmma	67	orthorhombic	{4,6,4,4,4}	12	(5,6)
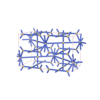
	sqc5951		Cmma	67	orthorhombic	{4,4,3,4,4}	14	(5,6)
	sqc5953		Cmma	67	orthorhombic	{4,4,3,8,4}	12	(5,6)
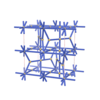
	sqc5958		Cmma	67	orthorhombic	{3,4,4,8,4}	12	(5,6)
	sqc5960		Cmma	67	orthorhombic	{8,3,4,4,4}	12	(5,6)
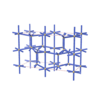
	sqc5967		Cmma	67	orthorhombic	{5,6}	10	(2,6)
	sqc5972		Cmma	67	orthorhombic	{4,6,4,4,4}	12	(5,6)
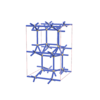
	sqc5976		Cmma	67	orthorhombic	{6,5}	10	(2,6)
	sqc5977		Cmma	67	orthorhombic	{6,5}	10	(2,6)
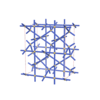
	sqc5979		Cmma	67	orthorhombic	{4,6,4,4,4}	12	(5,6)
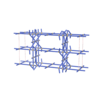
	sqc5982		Cmma	67	orthorhombic	{4,4,6,4,4}	12	(5,6)
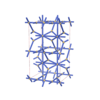
	sqc5984		Cmma	67	orthorhombic	{4,3,4,8,4}	12	(5,6)
	sqc5987		Cmma	67	orthorhombic	{8,4,3,4,4}	12	(5,6)
	sqc5994		Cmma	67	orthorhombic	{4,8,3,4,4}	12	(5,6)
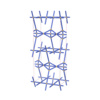
	sqc6000		Cmma	67	orthorhombic	{4,4,6,4,4}	12	(5,6)
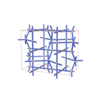
	sqc6001		Cmma	67	orthorhombic	{4,4,4,6,4}	12	(5,6)
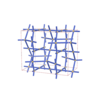
	sqc6003		Cmma	67	orthorhombic	{4,6,4,4,4}	12	(5,6)
	sqc6009		Cmma	67	orthorhombic	{4,4,4,6,4}	12	(5,6)
	sqc6012		Cmma	67	orthorhombic	{4,4,4,4,6}	12	(5,6)
	sqc6015		Cmma	67	orthorhombic	{4,6,4,4,4}	12	(5,6)
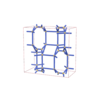
	sqc6019		Cmma	67	orthorhombic	{5,3}	12	(2,6)
	sqc6022		Cmma	67	orthorhombic	{6,5}	10	(2,6)
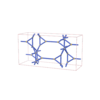
	sqc6030		Cmma	67	orthorhombic	{3,5}	12	(2,6)
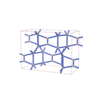
	sqc6033		Cmma	67	orthorhombic	{5,3}	12	(2,6)
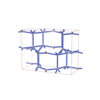
	sqc6036		Cmma	67	orthorhombic	{3,5}	12	(2,6)
	sqc6038		Cmma	67	orthorhombic	{5,3}	12	(2,6)
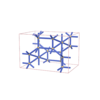
	sqc6040		Cmma	67	orthorhombic	{5,6}	10	(2,6)
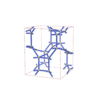
	sqc6043		Cmma	67	orthorhombic	{5,3}	12	(2,6)
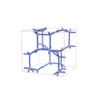
	sqc6046		Cmma	67	orthorhombic	{5,3}	12	(2,6)
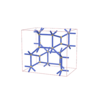
	sqc6054		Cmma	67	orthorhombic	{5,3}	12	(2,6)
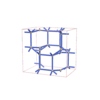
	sqc6055		Cmma	67	orthorhombic	{5,3}	12	(2,6)
	sqc6059		Cmma	67	orthorhombic	{3,5}	12	(2,6)
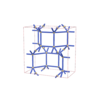
	sqc6061		Cmma	67	orthorhombic	{5,3}	12	(2,6)
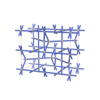
	sqc6080		Cmma	67	orthorhombic	{4,4,4,4,6}	12	(5,6)
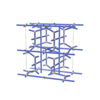
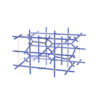
	sqc6085		Cmma	67	orthorhombic	{4,4,3,4,4}	14	(5,7)
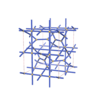
	sqc6092		Cmma	67	orthorhombic	{4,4,4,3,4}	14	(5,7)
	sqc6101		Cmma	67	orthorhombic	{3,4,4,4,4}	14	(5,7)
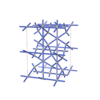
	sqc6103		Cmma	67	orthorhombic	{4,4,3,4,4}	14	(5,7)
	sqc6104		Cmma	67	orthorhombic	{4,4,6,4,4}	12	(5,6)
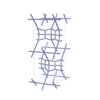
	sqc6105		Cmma	67	orthorhombic	{3,4,4,4,4}	14	(5,7)
	sqc6106		Cmma	67	orthorhombic	{3,4,4,4,4}	14	(5,6)
	sqc6108		Cmma	67	orthorhombic	{4,4,4,4,3}	14	(5,6)
	sqc6111		Cmma	67	orthorhombic	{4,3,4,4,4}	14	(5,6)
	sqc6113		Cmma	67	orthorhombic	{4,4,4,4,3}	14	(5,6)
	sqc6114		Cmma	67	orthorhombic	{4,3,4,4,4}	14	(5,6)
	sqc6250		Cmma	67	orthorhombic	{12,4}	10	(2,7)
	sqc6285		Cmma	67	orthorhombic	{8,3}	12	(2,7)
	sqc6289		Cmma	67	orthorhombic	{8,3}	12	(2,7)
	sqc6299		Cmma	67	orthorhombic	{4,8,4,4,4}	12	(5,7)
	sqc6302		Cmma	67	orthorhombic	{4,4,8,4,4}	12	(5,7)
	sqc6309		Cmma	67	orthorhombic	{6,4}	12	(2,7)