Cmma

Number	67
Symmetry Class	orthorhombic
Chiral	N

s-nets

872 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
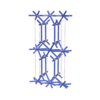
	sqc3253		Cmma	67	orthorhombic	{5,10}	6	(2,5)
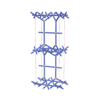
	sqc3265		Cmma	67	orthorhombic	{4,3,4,6}	10	(4,5)
	sqc3266		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,5)
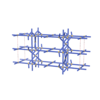
	sqc3267		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,5)
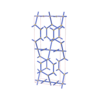
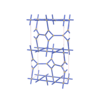
	sqc3269		Cmma	67	orthorhombic	{3,4,3,4}	12	(4,5)
	sqc3270		Cmma	67	orthorhombic	{4,3,4,3}	12	(4,5)
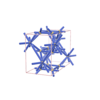
	sqc3273		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
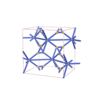
	sqc3286		Cmma	67	orthorhombic	{5,10}	6	(2,5)
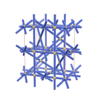
	sqc3343		Cmma	67	orthorhombic	{8,3}	10	(2,5)
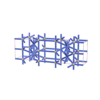
	sqc3375		Cmma	67	orthorhombic	{4,8,4,4}	8	(4,5)
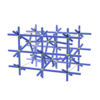
	sqc3377		Cmma	67	orthorhombic	{5,10}	6	(2,5)
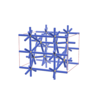
	sqc3380		Cmma	67	orthorhombic	{8,6}	6	(2,6)
	sqc3381		Cmma	67	orthorhombic	{6,8}	6	(2,6)
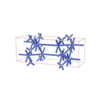
	sqc3382		Cmma	67	orthorhombic	{8,6}	6	(2,6)
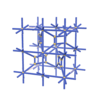
	sqc3384		Cmma	67	orthorhombic	{8,4}	6	(2,5)
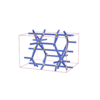
	sqc3386		Cmma	67	orthorhombic	{3,8}	10	(2,5)
	sqc3405		Cmma	67	orthorhombic	{6,4}	8	(2,6)
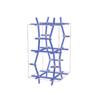
	sqc3415		Cmma	67	orthorhombic	{6,6,4,4}	8	(4,4)
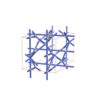
	sqc3418		Cmma	67	orthorhombic	{6,4}	8	(2,6)
	sqc3420		Cmma	67	orthorhombic	{4,6,3,4}	10	(4,5)
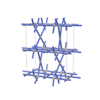
	sqc3434		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,5)
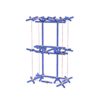
	sqc3447		Cmma	67	orthorhombic	{8,4}	6	(2,5)
	sqc3453		Cmma	67	orthorhombic	{4,6}	8	(2,6)
	sqc3456		Cmma	67	orthorhombic	{5,5}	8	(2,5)
	sqc3462		Cmma	67	orthorhombic	{8,4}	6	(2,5)
	sqc3463		Cmma	67	orthorhombic	{4,8}	6	(2,5)
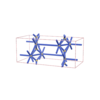
	sqc3464		Cmma	67	orthorhombic	{8,4}	6	(2,5)
	sqc3467		Cmma	67	orthorhombic	{6,7}	6	(2,5)
	sqc3469		Cmma	67	orthorhombic	{7,3}	8	(2,5)
	sqc3470		Cmma	67	orthorhombic	{7,3}	8	(2,5)
	sqc3472		Cmma	67	orthorhombic	{4,6}	8	(2,6)
	sqc3489		Cmma	67	orthorhombic	{6,7}	6	(2,6)
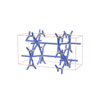
	sqc3490		Cmma	67	orthorhombic	{3,7}	8	(2,6)
	sqc3491		Cmma	67	orthorhombic	{7,3}	8	(2,6)
	sqc3492		Cmma	67	orthorhombic	{3,7}	8	(2,6)
	sqc3497		Cmma	67	orthorhombic	{6,8}	6	(2,6)
	sqc3499		Cmma	67	orthorhombic	{6,4}	8	(2,6)
	sqc3500		Cmma	67	orthorhombic	{6,4}	8	(2,6)
	sqc3527		Cmma	67	orthorhombic	{6,7}	6	(2,5)
	sqc3528		Cmma	67	orthorhombic	{3,7}	8	(2,5)
	sqc3529		Cmma	67	orthorhombic	{7,3}	8	(2,5)
	sqc3531		Cmma	67	orthorhombic	{6,4}	8	(2,6)
	sqc3551		Cmma	67	orthorhombic	{8,4}	6	(2,5)
	sqc3552		Cmma	67	orthorhombic	{7,6}	6	(2,6)
	sqc3553		Cmma	67	orthorhombic	{7,3}	8	(2,6)
	sqc3556		Cmma	67	orthorhombic	{6,6,4,4}	8	(4,4)
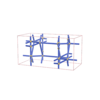
	sqc3563		Cmma	67	orthorhombic	{6,4}	8	(2,6)
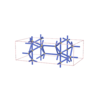
	sqc3569		Cmma	67	orthorhombic	{6,4}	8	(2,6)
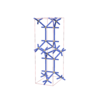
	sqc3586		Cmma	67	orthorhombic	{5,5}	8	(2,5)
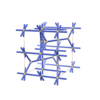
	sqc3592		Cmma	67	orthorhombic	{5,5}	8	(2,5)
	sqc3595		Cmma	67	orthorhombic	{6,3,4,4}	10	(4,5)
	sqc3605		Cmma	67	orthorhombic	{4,8,4}	8	(3,6)
	sqc3659		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,6)
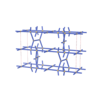
	sqc3676		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
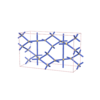
	sqc3685		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
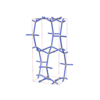
	sqc3689		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
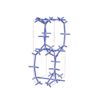
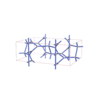
	sqc3696		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,5)
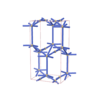
	sqc3700		Cmma	67	orthorhombic	{3,4,3,4}	12	(4,5)
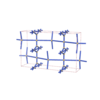
	sqc3711		Cmma	67	orthorhombic	{4,6}	8	(2,6)
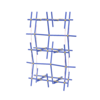
	sqc3712		Cmma	67	orthorhombic	{6,3,4,4}	10	(4,5)
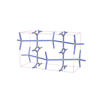
	sqc3713		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,6)
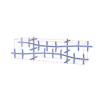
	sqc3714		Cmma	67	orthorhombic	{3,4,3,4}	12	(4,5)
	sqc3715		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,6)
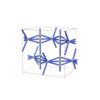
	sqc3716		Cmma	67	orthorhombic	{3,3,4,4}	12	(4,5)
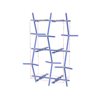
	sqc3719		Cmma	67	orthorhombic	{4,8,4}	8	(3,5)
	sqc3720		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,5)
	sqc3736		Cmma	67	orthorhombic	{6,4}	8	(2,6)
	sqc3742		Cmma	67	orthorhombic	{4,6,3,4}	10	(4,5)
	sqc3745		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
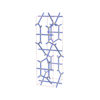
	sqc3746		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
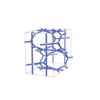
	sqc3749		Cmma	67	orthorhombic	{3,3,4,4}	12	(4,5)
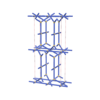
	sqc3758		Cmma	67	orthorhombic	{3,6,4,4}	10	(4,5)
	sqc3772		Cmma	67	orthorhombic	{4,6,3,4}	10	(4,5)
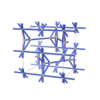
	sqc3773		Cmma	67	orthorhombic	{4,3,4,6}	10	(4,5)
	sqc3774		Cmma	67	orthorhombic	{4,8,4}	8	(3,5)
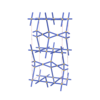
	sqc3821		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,5)
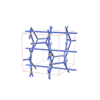
	sqc3825		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,5)
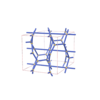
	sqc3827		Cmma	67	orthorhombic	{3,4,3,4}	12	(4,5)
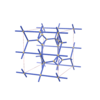
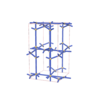
	sqc3830		Cmma	67	orthorhombic	{3,4,3,4}	12	(4,5)
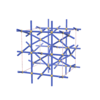
	sqc3842		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
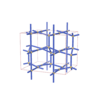
	sqc3843		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,5)
	sqc3845		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
	sqc3848		Cmma	67	orthorhombic	{4,4}	10	(2,4)
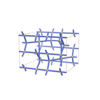
	sqc3860		Cmma	67	orthorhombic	{4,4,4,4}	10	(4,5)
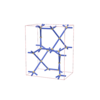
	sqc3861		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
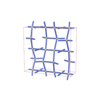
	sqc3863		Cmma	67	orthorhombic	{4,4}	10	(2,4)
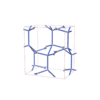
	sqc3876		Cmma	67	orthorhombic	{4,4,4}	10	(3,6)
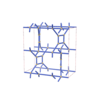
	sqc3885		Cmma	67	orthorhombic	{3,4}	12	(2,5)
	sqc3886		Cmma	67	orthorhombic	{4,3}	12	(2,5)
	sqc4044		Cmma	67	orthorhombic	{10,6}	6	(2,6)
	sqc4053		Cmma	67	orthorhombic	{8,4,4,6}	8	(4,5)
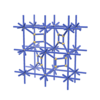
	sqc4063		Cmma	67	orthorhombic	{10,3}	10	(2,6)
	sqc4078		Cmma	67	orthorhombic	{8,6,4,4}	8	(4,5)
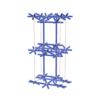
	sqc4115		Cmma	67	orthorhombic	{6,8}	6	(2,6)
	sqc4116		Cmma	67	orthorhombic	{3,8}	8	(2,6)
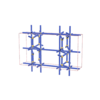
	sqc4117		Cmma	67	orthorhombic	{3,8}	8	(2,6)
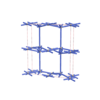
	sqc4127		Cmma	67	orthorhombic	{6,8}	6	(2,6)
	sqc4128		Cmma	67	orthorhombic	{3,8}	8	(2,6)
	sqc4129		Cmma	67	orthorhombic	{8,3}	8	(2,6)
	sqc4130		Cmma	67	orthorhombic	{7,4}	8	(2,6)