Fddd

Number	70
Symmetry Class	orthorhombic
Chiral	N

s-nets

816 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
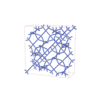
	sqc8739		Fddd	70	orthorhombic	{5,4}	16	(2,6)
	sqc8744		Fddd	70	orthorhombic	{5,4}	16	(2,6)
	sqc8753		Fddd	70	orthorhombic	{4,8,3}	16	(3,6)
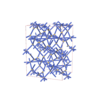
	sqc8754		Fddd	70	orthorhombic	{3,8,4}	16	(3,6)
	sqc8760		Fddd	70	orthorhombic	{4,6,4}	16	(3,6)
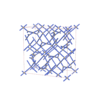
	sqc8762		Fddd	70	orthorhombic	{4,4,3,4}	20	(4,5)
	sqc8780		Fddd	70	orthorhombic	{3,8,4}	16	(3,6)
	sqc8781		Fddd	70	orthorhombic	{4,8,3}	16	(3,6)
	sqc8782		Fddd	70	orthorhombic	{4,8,3}	16	(3,6)
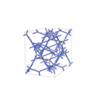
	sqc8783		Fddd	70	orthorhombic	{3,8,4}	16	(3,6)
	sqc8784		Fddd	70	orthorhombic	{4,4,6}	16	(3,6)
	sqc8785		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc8786		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc8789		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc8791		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc8799		Fddd	70	orthorhombic	{4,6,4}	16	(3,6)
	sqc8800		Fddd	70	orthorhombic	{4,6,4}	16	(3,6)
	sqc8803		Fddd	70	orthorhombic	{4,4,3,4}	20	(4,5)
	sqc8804		Fddd	70	orthorhombic	{4,4,3,4}	20	(4,5)
	sqc8805		Fddd	70	orthorhombic	{4,4,6}	16	(3,6)
	sqc8806		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc8808		Fddd	70	orthorhombic	{4,4,6}	16	(3,6)
	sqc8810		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc8811		Fddd	70	orthorhombic	{6,4,4}	16	(3,6)
	sqc8814		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc8815		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc8816		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc8817		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc8818		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc8819		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc8821		Fddd	70	orthorhombic	{8,3,4}	16	(3,6)
	sqc8823		Fddd	70	orthorhombic	{8,3,4}	16	(3,6)
	sqc8824		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc8827		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc8828		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc8830		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc8831		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc8832		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc8850		Fddd	70	orthorhombic	{8,6,4}	12	(3,5)
	sqc8851		Fddd	70	orthorhombic	{8,3,4}	16	(3,6)
	sqc8853		Fddd	70	orthorhombic	{7,4}	12	(2,5)
	sqc8854		Fddd	70	orthorhombic	{7,4}	12	(2,5)
	sqc8859		Fddd	70	orthorhombic	{3,8,4}	16	(3,6)
	sqc8860		Fddd	70	orthorhombic	{3,8,4}	16	(3,6)
	sqc8864		Fddd	70	orthorhombic	{4,8,3}	16	(3,6)
	sqc8865		Fddd	70	orthorhombic	{4,8,3}	16	(3,6)
	sqc8869		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8871		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8872		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8874		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8879		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8880		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8881		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8882		Fddd	70	orthorhombic	{4,4,6}	16	(3,6)
	sqc8889		Fddd	70	orthorhombic	{5,4}	16	(2,6)
	sqc8890		Fddd	70	orthorhombic	{5,4}	16	(2,6)
	sqc8891		Fddd	70	orthorhombic	{5,4}	16	(2,6)
	sqc8909		Fddd	70	orthorhombic	{6,4,4}	16	(3,6)
	sqc8918		Fddd	70	orthorhombic	{4,4,6}	16	(3,6)
	sqc8923		Fddd	70	orthorhombic	{6,3,3}	20	(3,5)
	sqc8927		Fddd	70	orthorhombic	{6,3,3}	20	(3,5)
	sqc8932		Fddd	70	orthorhombic	{8,6,4}	12	(3,5)
	sqc9000		Fddd	70	orthorhombic	{4,6,4}	16	(3,6)
	sqc9002		Fddd	70	orthorhombic	{4,6,4}	16	(3,6)
	sqc9131		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc9133		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc9134		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc9135		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc9162		Fddd	70	orthorhombic	{4,4,3,4}	20	(4,5)
	sqc9163		Fddd	70	orthorhombic	{4,4,3,4}	20	(4,5)
	sqc9164		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc9165		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc9166		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc9167		Fddd	70	orthorhombic	{4,4,3}	20	(3,6)
	sqc9168		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc9169		Fddd	70	orthorhombic	{3,4,4}	20	(3,6)
	sqc9226		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc9227		Fddd	70	orthorhombic	{4,3,4}	20	(3,6)
	sqc9391		Fddd	70	orthorhombic	{5,10}	12	(2,6)
	sqc9392		Fddd	70	orthorhombic	{5,10}	12	(2,6)
	sqc9394		Fddd	70	orthorhombic	{5,10}	12	(2,6)
	sqc9402		Fddd	70	orthorhombic	{8,3,3}	20	(3,6)
	sqc9424		Fddd	70	orthorhombic	{5,10}	12	(2,6)
	sqc9425		Fddd	70	orthorhombic	{5,10}	12	(2,6)
	sqc9468		Fddd	70	orthorhombic	{8,4}	12	(2,6)
	sqc9472		Fddd	70	orthorhombic	{3,7}	16	(2,6)
	sqc9484		Fddd	70	orthorhombic	{8,4}	12	(2,6)
	sqc9485		Fddd	70	orthorhombic	{8,4}	12	(2,6)
	sqc9486		Fddd	70	orthorhombic	{8,3,3}	20	(3,6)
	sqc9487		Fddd	70	orthorhombic	{6,7}	12	(2,6)
	sqc9488		Fddd	70	orthorhombic	{6,7}	12	(2,6)
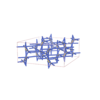
	sqc9489		Fddd	70	orthorhombic	{3,7}	16	(2,6)
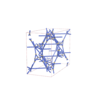
	sqc9490		Fddd	70	orthorhombic	{4,6}	16	(2,6)
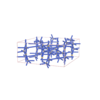
	sqc9495		Fddd	70	orthorhombic	{8,3,3}	20	(3,6)
	sqc9496		Fddd	70	orthorhombic	{6,7}	12	(2,6)
	sqc9497		Fddd	70	orthorhombic	{3,7}	16	(2,6)
	sqc9498		Fddd	70	orthorhombic	{3,7}	16	(2,6)
	sqc9502		Fddd	70	orthorhombic	{8,4}	12	(2,6)
	sqc9503		Fddd	70	orthorhombic	{8,4}	12	(2,6)
	sqc9504		Fddd	70	orthorhombic	{8,8,4}	12	(3,6)