Fddd

Number	70
Symmetry Class	orthorhombic
Chiral	N

s-nets

816 records listed.

Image	s-net name	Other names	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
	sqc7809		Fddd	70	orthorhombic	{4,3,3}	20	(3,5)
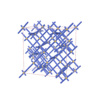
	sqc7812		Fddd	70	orthorhombic	{4,6}	12	(2,5)
	sqc7817		Fddd	70	orthorhombic	{4,8}	12	(2,6)
	sqc7822		Fddd	70	orthorhombic	{8,4,4}	12	(3,5)
	sqc7823		Fddd	70	orthorhombic	{8,4,4}	12	(3,5)
	sqc7825		Fddd	70	orthorhombic	{6,4}	12	(2,5)
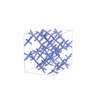
	sqc7826		Fddd	70	orthorhombic	{6,4}	12	(2,5)
	sqc7827		Fddd	70	orthorhombic	{6,4}	12	(2,5)
	sqc7828		Fddd	70	orthorhombic	{6,5}	12	(2,5)
	sqc7830		Fddd	70	orthorhombic	{6,4}	12	(2,5)
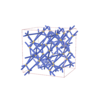
	sqc7833		Fddd	70	orthorhombic	{6,5}	12	(2,5)
	sqc7836		Fddd	70	orthorhombic	{6,3,4}	16	(3,5)
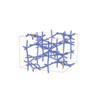
	sqc7837		Fddd	70	orthorhombic	{6,3,4}	16	(3,5)
	sqc7839		Fddd	70	orthorhombic	{6,5}	12	(2,5)
	sqc7842		Fddd	70	orthorhombic	{6,5}	12	(2,5)
	sqc7847		Fddd	70	orthorhombic	{3,5}	16	(2,5)
	sqc7848		Fddd	70	orthorhombic	{3,5}	16	(2,5)
	sqc7853		Fddd	70	orthorhombic	{3,3,4}	20	(3,5)
	sqc7854		Fddd	70	orthorhombic	{4,3,3}	20	(3,5)
	sqc7865		Fddd	70	orthorhombic	{4,8}	12	(2,6)
	sqc7874		Fddd	70	orthorhombic	{6,5}	12	(2,5)
	sqc7884		Fddd	70	orthorhombic	{6,6,4}	12	(3,5)
	sqc7885		Fddd	70	orthorhombic	{6,6,4}	12	(3,5)
	sqc7887		Fddd	70	orthorhombic	{6,3,4}	16	(3,5)
	sqc7890		Fddd	70	orthorhombic	{6,3,4}	16	(3,5)
	sqc7892		Fddd	70	orthorhombic	{6,3,4}	16	(3,5)
	sqc7897		Fddd	70	orthorhombic	{4,3,6}	16	(3,5)
	sqc7898		Fddd	70	orthorhombic	{6,3,4}	16	(3,5)
	sqc7968		Fddd	70	orthorhombic	{4,6,3}	16	(3,5)
	sqc7969		Fddd	70	orthorhombic	{4,6,3}	16	(3,5)
	sqc7970		Fddd	70	orthorhombic	{3,6,4}	16	(3,5)
	sqc7971		Fddd	70	orthorhombic	{3,6,4}	16	(3,5)
	sqc8047		Fddd	70	orthorhombic	{4,4,4}	16	(3,5)
	sqc8049		Fddd	70	orthorhombic	{4,4,4}	16	(3,5)
	sqc8087		Fddd	70	orthorhombic	{4,4,4}	16	(3,5)
	sqc8093		Fddd	70	orthorhombic	{4,4,4}	16	(3,5)
	sqc8100		Fddd	70	orthorhombic	{4,4}	16	(2,6)
	sqc8110		Fddd	70	orthorhombic	{4,4}	16	(2,6)
	sqc8474		Fddd	70	orthorhombic	{12,3}	12	(2,6)
	sqc8475		Fddd	70	orthorhombic	{12,3}	12	(2,6)
	sqc8476		Fddd	70	orthorhombic	{3,12}	12	(2,6)
	sqc8477		Fddd	70	orthorhombic	{3,12}	12	(2,6)
	sqc8478		Fddd	70	orthorhombic	{10,4}	12	(2,6)
	sqc8479		Fddd	70	orthorhombic	{3,12}	12	(2,6)
	sqc8481		Fddd	70	orthorhombic	{10,4}	12	(2,6)
	sqc8485		Fddd	70	orthorhombic	{10,4}	12	(2,6)
	sqc8499		Fddd	70	orthorhombic	{5,8}	12	(2,6)
	sqc8500		Fddd	70	orthorhombic	{8,3,4}	16	(3,6)
	sqc8523		Fddd	70	orthorhombic	{12,3}	12	(2,6)
	sqc8526		Fddd	70	orthorhombic	{3,12}	12	(2,6)
	sqc8527		Fddd	70	orthorhombic	{12,3}	12	(2,6)
	sqc8541		Fddd	70	orthorhombic	{10,4}	12	(2,6)
	sqc8542		Fddd	70	orthorhombic	{3,12}	12	(2,6)
	sqc8567		Fddd	70	orthorhombic	{12,3}	12	(2,6)
	sqc8583		Fddd	70	orthorhombic	{10,4}	12	(2,6)
	sqc8631		Fddd	70	orthorhombic	{8,3,4}	16	(3,6)
	sqc8632		Fddd	70	orthorhombic	{5,8}	12	(2,6)
	sqc8633		Fddd	70	orthorhombic	{5,8}	12	(2,6)
	sqc8634		Fddd	70	orthorhombic	{7,4}	12	(2,5)
	sqc8635		Fddd	70	orthorhombic	{7,4}	12	(2,5)
	sqc8640		Fddd	70	orthorhombic	{7,4}	12	(2,5)
	sqc8644		Fddd	70	orthorhombic	{8,6,4}	12	(3,5)
	sqc8648		Fddd	70	orthorhombic	{8,6,4}	12	(3,5)
	sqc8649		Fddd	70	orthorhombic	{8,6,4}	12	(3,5)
	sqc8657		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8659		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8660		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8661		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8665		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8669		Fddd	70	orthorhombic	{6,4,4}	16	(3,6)
	sqc8670		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8676		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8677		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8678		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8681		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8683		Fddd	70	orthorhombic	{6,4,4}	16	(3,6)
	sqc8684		Fddd	70	orthorhombic	{6,4,4}	16	(3,6)
	sqc8685		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8689		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8691		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8693		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8694		Fddd	70	orthorhombic	{6,6}	12	(2,6)
	sqc8697		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8700		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8703		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8706		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8707		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8708		Fddd	70	orthorhombic	{6,3,3}	20	(3,5)
	sqc8711		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8712		Fddd	70	orthorhombic	{6,3}	16	(2,6)
	sqc8715		Fddd	70	orthorhombic	{3,6}	16	(2,6)
	sqc8716		Fddd	70	orthorhombic	{6,3,3}	20	(3,5)
	sqc8717		Fddd	70	orthorhombic	{6,3,3}	20	(3,5)
	sqc8726		Fddd	70	orthorhombic	{5,8}	12	(2,6)
	sqc8727		Fddd	70	orthorhombic	{5,8}	12	(2,6)
	sqc8729		Fddd	70	orthorhombic	{5,4}	16	(2,6)
	sqc8730		Fddd	70	orthorhombic	{5,4}	16	(2,6)
	sqc8733		Fddd	70	orthorhombic	{5,4}	16	(2,6)
	sqc8735		Fddd	70	orthorhombic	{5,4}	16	(2,6)
	sqc8737		Fddd	70	orthorhombic	{5,4}	16	(2,6)