s-net search

Glossary of terms

s-net name	e.g. sqc5432
Other name
Symmetry class
Space group
Vertex transitivity
Edge transitivity
Vertices per primitive unit cell
Vertex degree(s)
Coordination sequence	any subsequence separated by spaces e.g. 4 12 30
Shortest cycle

14646 records listed.

s-net name	Space group	Space group number	Symmetry class	Vertex degree(s)	Vertices per primitive unit cell	Transitivity (Vertex, Edge)
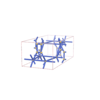
sqc5800	Imma	74	orthorhombic	{7,3}	12	(2,7)
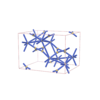
sqc5801	C2/c	15	monoclinic	{7,3,3}	12	(3,7)
sqc5802	C2/c	15	monoclinic	{4,4,8,6,4}	10	(5,7)
sqc5803	Imma	74	orthorhombic	{4,4,8,6,4}	10	(5,6)
sqc5804	Imma	74	orthorhombic	{4,4,8,6,4}	10	(5,6)
sqc5805	P-4m2	115	tetragonal	{7,3}	12	(2,6)
sqc5806	P42/mmc	131	tetragonal	{7,3}	12	(2,4)
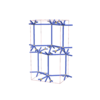
sqc5807	Cmma	67	orthorhombic	{7,3}	12	(2,7)
sqc5808	C2/c	15	monoclinic	{8,6,4,4,4}	10	(5,7)
sqc5809	Imma	74	orthorhombic	{8,6,4,4,4}	10	(5,6)
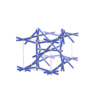
sqc5810	P4222	93	tetragonal	{4,4,4,4,6}	12	(5,6)
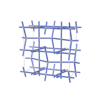
sqc5811	Cmma	67	orthorhombic	{4,4,4,4,6}	12	(5,6)
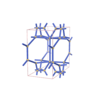
sqc5812	Pmmm	47	orthorhombic	{3,4,7,4,4}	12	(5,7)
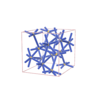
sqc5813	C2/c	15	monoclinic	{7,6}	8	(2,8)
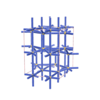
sqc5814	Imma	74	orthorhombic	{6,7}	8	(2,7)
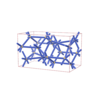
sqc5815	C2/c	15	monoclinic	{6,7}	8	(2,8)
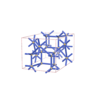
sqc5816	Imma	74	orthorhombic	{6,5}	10	(2,6)
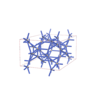
sqc5817	Fmmm	69	orthorhombic	{5,6}	10	(2,6)
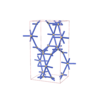
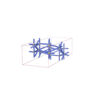
sqc5818	Cmma	67	orthorhombic	{5,6}	10	(2,6)
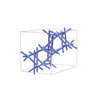
sqc5819	Imma	74	orthorhombic	{6,5}	10	(2,6)
sqc5820	C2/c	15	monoclinic	{6,5,5}	10	(3,7)
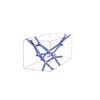
sqc5821	I212121	24	orthorhombic	{6,5,5}	10	(3,7)
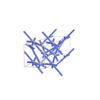
sqc5822	P4222	93	tetragonal	{5,3}	12	(2,6)
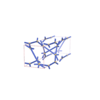
sqc5823	P4222	93	tetragonal	{5,6}	10	(2,6)
sqc5824	P4222	93	tetragonal	{3,5}	12	(2,6)
sqc5825	P4222	93	tetragonal	{3,5}	12	(2,6)
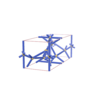
sqc5826	Cmma	67	orthorhombic	{5,8}	8	(2,7)
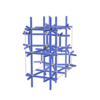
sqc5827	P4222	93	tetragonal	{5,6}	10	(2,6)
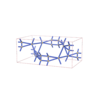
sqc5828	Imma	74	orthorhombic	{8,5}	8	(2,7)
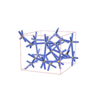
sqc5829	Cmma	67	orthorhombic	{4,5}	12	(2,6)
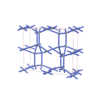
sqc5830	I212121	24	orthorhombic	{6,5,5}	10	(3,7)
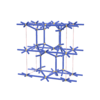
sqc5831	Cmma	67	orthorhombic	{6,5}	10	(2,6)
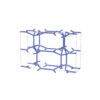
sqc5832	Cmma	67	orthorhombic	{6,5}	10	(2,6)
sqc5833	Cmma	67	orthorhombic	{3,5}	12	(2,6)
sqc5834	Imma	74	orthorhombic	{5,4}	12	(2,6)
sqc5835	C2/c	15	monoclinic	{8,5}	8	(2,8)
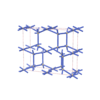
sqc5836	C2/c	15	monoclinic	{6,5,5}	10	(3,7)
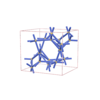
sqc5837	Cmma	67	orthorhombic	{6,5}	10	(2,6)
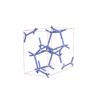
sqc5838	C2/c	15	monoclinic	{6,5,5}	10	(3,7)
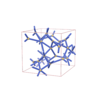
sqc5839	C2/c	15	monoclinic	{5,4,4}	12	(3,7)
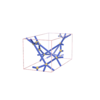
sqc5840	I212121	24	orthorhombic	{3,5,5}	12	(3,7)
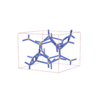
sqc5841	P4222	93	tetragonal	{5,3}	12	(2,6)
sqc5842	C2/c	15	monoclinic	{3,5,5}	12	(3,7)
sqc5843	Fmmm	69	orthorhombic	{4,5}	12	(2,6)
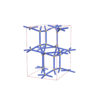
sqc5844	Fmmm	69	orthorhombic	{5,4}	12	(2,6)
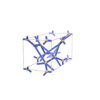
sqc5845	Cmma	67	orthorhombic	{4,5}	12	(2,6)
sqc5846	P4222	93	tetragonal	{5,3}	12	(2,6)
sqc5847	C2/c	15	monoclinic	{5,4,4}	12	(3,7)
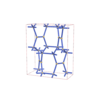
sqc5848	Cmma	67	orthorhombic	{3,5}	12	(2,6)
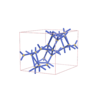
sqc5849	C2/c	15	monoclinic	{3,5,5}	12	(3,7)
sqc5850	Cmma	67	orthorhombic	{4,5}	12	(2,6)
sqc5851	Cmma	67	orthorhombic	{5,4}	12	(2,6)
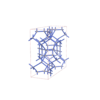
sqc5852	Fmmm	69	orthorhombic	{5,4}	12	(2,6)
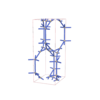
sqc5853	Cmma	67	orthorhombic	{5,4}	12	(2,6)
sqc5854	I212121	24	orthorhombic	{5,4,4}	12	(3,7)
sqc5855	C2/c	15	monoclinic	{4,8,6,4,4}	10	(5,7)
sqc5856	C2/c	15	monoclinic	{4,4,8,6,4}	10	(5,7)
sqc5857	C2/c	15	monoclinic	{3,4,4,4,4}	14	(5,8)
sqc5858	C2/c	15	monoclinic	{4,4,4,4,3}	14	(5,8)
sqc5859	C2/c	15	monoclinic	{4,3,4,4,4}	14	(5,8)
sqc5860	Imma	74	orthorhombic	{4,8,6,4,4}	10	(5,6)
sqc5861	I212121	24	orthorhombic	{4,8,3,4,4}	12	(5,7)
sqc5862	Imma	74	orthorhombic	{4,4,8,6,4}	10	(5,6)
sqc5863	Imma	74	orthorhombic	{4,4,4,4,3}	14	(5,7)
sqc5864	Imma	74	orthorhombic	{3,4,4,4,4}	14	(5,7)
sqc5865	Imma	74	orthorhombic	{4,3,4,4,4}	14	(5,7)
sqc5866	C2/c	15	monoclinic	{4,8,3,4,4}	12	(5,7)
sqc5867	Imma	74	orthorhombic	{4,8,3,4,4}	12	(5,6)
sqc5868	I212121	24	orthorhombic	{4,4,8,6,4}	10	(5,7)
sqc5869	I212121	24	orthorhombic	{4,4,4,4,3}	14	(5,8)
sqc5870	I212121	24	orthorhombic	{3,4,4,4,4}	14	(5,8)
sqc5871	I212121	24	orthorhombic	{4,3,4,4,4}	14	(5,8)
sqc5872	Imma	74	orthorhombic	{4,3,4,4,4}	14	(5,7)
sqc5873	Imma	74	orthorhombic	{4,4,4,3,4}	14	(5,7)
sqc5874	C2/c	15	monoclinic	{4,3,4,4,4}	14	(5,8)
sqc5875	C2/c	15	monoclinic	{4,4,4,3,4}	14	(5,8)
sqc5876	I212121	24	orthorhombic	{4,4,4,3,4}	14	(5,8)
sqc5877	I212121	24	orthorhombic	{4,3,4,4,4}	14	(5,8)
sqc5878	I212121	24	orthorhombic	{3,4,4,4,4}	14	(5,8)
sqc5879	C2/c	15	monoclinic	{4,4,4,6,4}	12	(5,7)
sqc5880	I212121	24	orthorhombic	{4,4,4,6,4}	12	(5,7)
sqc5881	I212121	24	orthorhombic	{3,4,4,4,4}	14	(5,8)
sqc5882	Imma	74	orthorhombic	{4,4,4,6,4}	12	(5,6)
sqc5883	C2/c	15	monoclinic	{3,4,4,4,4}	14	(5,8)
sqc5884	C2/c	15	monoclinic	{3,4,4,4,4}	14	(5,8)
sqc5885	Imma	74	orthorhombic	{3,4,4,4,4}	14	(5,7)
sqc5886	Imma	74	orthorhombic	{3,4,4,4,4}	14	(5,7)
sqc5887	C2/c	15	monoclinic	{4,3,4,4,4}	14	(5,8)
sqc5888	I212121	24	orthorhombic	{4,4,3,4,4}	14	(5,8)
sqc5889	Imma	74	orthorhombic	{4,3,4,4,4}	14	(5,7)
sqc5890	Imma	74	orthorhombic	{4,4,3,4,4}	14	(5,7)
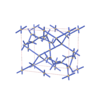
sqc5891	I212121	24	orthorhombic	{4,3,4,4,4}	14	(5,8)
sqc5892	C2/c	15	monoclinic	{4,4,3,4,4}	14	(5,8)
sqc5893	Fmmm	69	orthorhombic	{4,3,8,4,4}	12	(5,6)
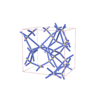
sqc5894	Fmmm	69	orthorhombic	{4,6,4,4,4}	12	(5,6)
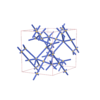
sqc5895	I212121	24	orthorhombic	{4,4,6,4,4}	12	(5,7)
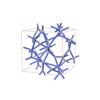
sqc5896	C2/c	15	monoclinic	{4,4,6,4,4}	12	(5,7)
sqc5897	I212121	24	orthorhombic	{4,6,4,4,4}	12	(5,7)
sqc5898	C2/c	15	monoclinic	{4,6,4,4,4}	12	(5,7)
sqc5899	P4/mmm	123	tetragonal	{3,6,4}	12	(3,5)