2D Hyperbolic Tilings

As in the euclidean plane ( E² ), there is a natural correspondence between periodic networks in the hyperbolic plane ( H² ) and the edge skeletons of periodic tilings by polygons. We therefore achieve an enumeration of hyperbolic nets by enumerating 2D hyperbolic tilings, since this allows us to use the efficient algorithms developed within combinatorial tiling theory .

The first step in enumerating the tilings that can be mapped onto a given TPMS is to find all the hyperbolic symmetry groups that are compatible with the chosen set of symmetries of the periodic minimal surface .

For the P surface this means finding subgroups of the *246 reflection group that retain the translational periodicity of the unit cell. We find these groups using the computational discrete algebra package GAP. The process is explained in detail in our paper “2D hyperbolic groups induce 3–periodic euclidean reticulations” Eur. Phys. J. B 39:365–375 [DOI link]. The list of symmetry groups for the P,D, and G surfaces is also collated online. We always refer to symmetry groups using Conway's orbifold symbol .

The symmetry and topology of a 2D tiling are compactly encoded by a Delaney–Dress symbol . These symbols represent a discrete structure on an orbifold . Thus, the enumeration of tilings proceeds by the systematic enumeration all possible triangulations of a given orbifold . An overview of the algorithms (due to Huson and Delgado–Friedrichs) is given here . To keep the Epinet database at a manageable size, we have restricted our enumeration to tilings with one and two types of tile ( tile–1–transitive and tile–2–transitive tilings ) and their duals (vertex–1–transitive and vertex–2–transitive tilings).

A Delaney–Dress symbol is an abstract combinatorial description of a tiling, so the next step is to give it a geometric realisation in the hyperbolic plane ( H² ). The embedding must be compatible with the symmetries of the covering map , and this requirement introduces some degeneracies (two or more Delaney–Dress symbols mapping to the same geometric realisation), and also some new distinctions (one Delaney–Dress symbol may have many geometric realisations that give distinct surface reticulations ). The detection of these possibilities is described in the paper "3D Euclidean networks from 2D hyperbolic tilings with kaleidoscopic symmetry". [DOI link]

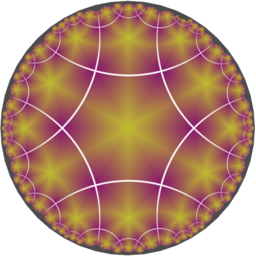
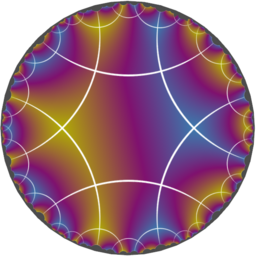
The three tilings below all have the topology of four hexagons meeting around each vertex. Even though the edge skeleton of the tiling on the left is identical to that on the right, the two have different Delaney-Dress symbols because they have different symmetries. The tiling in the middle has exactly the same Delaney-Dress symbol as the one on the right, and both have symmetry *222222 (*2^6). However, there are two distinct (non-conjugate) subgroups of *246 with this orbifold and so there are two non-isometric ways to draw the tiling within the *246 grid.

*246	*222222a	*222222b

There is another way in which a single Delaney-Dress symbol can generate more than one distinct surface reticulation — even within the same subgroup. On the individual tiling pages these are referred to as “automorphic tilings&rdquo. This situation occurs when the orbifold symbol has some symmetry (an automorphism) that is broken when the orbifold is represented as a subgroup of *246. For example, the abstract *2224 orbifold is a kite shape with three types of vertex (one *4 and two types of *2 corner points) and two types of edge (one joining a *4 to a *2, and the other, a *2 to a *2). When embedded within *246, however, all corners and edges are distinct. Therefore, there may be non-isometric embeddings of a single Delaney-Dress symbol. In particular, the Delaney-Dress symbols for a tiling derived from a glue or split operation involving any single edge will have two distinct embeddings in H² , as will any glue or split operation involving one of the *2 corners adjacent to the *4. A glue around the *4 corner has only one embedding, however, because there is only one *4 corner in the orbifold so there is no symmetry to break. The following images illustrate an edge-glue example.

*2224 fundamental tiling	*2224_FG_4 embedding 1	*2224_FG_4 embedding 2

Return to the EPINET mathematical background page.