Covering Maps of Triply Periodic Minimal Surfaces

The starting point in our enumeration is a triply periodic minimal surface (TPMS) . These surfaces have the hyperbolic plane ( H² ) as their universal covering space . This means that there is a continuous map from the hyperbolic plane ( H² ) onto the surface such that a small patch of the surface pulls back to a countable number of isomorphic copies in the hyperbolic plane.

The following sequence of images shows how the hyperbolic plane wraps onto the P minimal surface .

Step 1	Step 2	Step 3

Step 4	Step 5	Step 6

Step 7

To proceed with our enumeration of surface reticulations , we need a covering map , that respects the symmetries of the TPMS (or at least some chosen subgroup of symmetries). Within EPINET, we are interested in translationally–periodic structures, so we use covering maps , that are based on the smallest translational unit that doesn't exchange the two sides of the surface.

Consider once more Schwarz's P (primitive) surface , for example. A translational unit cell for the P surface can be as small as the portion on the left in the illustration below, (a translational unit for the non-oriented surface), or large enough to incorporate many of these units (as the figure on the right in the illustration shows). The translational unit cell we use within EPINET is shown in the middle of the illustration below.

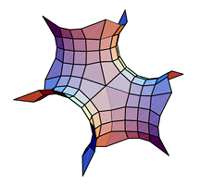
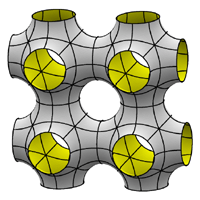
P surface: non-oriented unit cell	P surface: oriented unit cell	P surface: four oriented unit cells

The TPMS we use also have a high degree of intrinsic symmetry, so it is convenient to work with a covering map that respects these higher symmetries of the surface. For the P (primitive) , surface and its close relatives, the D (diamond) and G (gyroid) surfaces, the intrinsic surface symmetries have a natural representation in the hyperbolic plane as a group of reflections in the sides of a triangle with angles π/2 , π/4 , and π/6 . We use Conway's orbifold notation , and refer to this group as *246 .

H² dodecagon	P surface

G surface	D surface

Now we have a well–defined map from the hyperbolic plane onto a TPMS , which also respects the chosen symmetries of the surface. This allows us to work in the hyperbolic plane where the mathematics of tilings and symmetry is much simpler. To get the corresponding three–dimensional structures, we use the covering map to project the hyperbolic patterns onto the TPMS .

Return to the EPINET mathematical background page.